The Inverted
Correlation Matrix --
![]()
The determinant of the correlation matrix will equal 1.0 only if all correlations equal 0, otherwise the determinant will be less than 1. Remember that the determinant is related to the volume of the space occupied by the swarm of data points represen ted by standard scores on the measures involved. When the measures are uncorrelated, this space is a sphere with a volume of 1. When the measures are correlated, the space occupied becomes an ellipsoid whose volume is less than 1.
Because the correlation matrix is symmetric, its inverse is also symmetric. The diagonal elements of the inverted correlation matrix, ![]() , will be larger than 1.0. If the correlations in R are all
positive, most of the off diagonal elements in
, will be larger than 1.0. If the correlations in R are all
positive, most of the off diagonal elements in ![]() will be negative. Each element in
will be negative. Each element in ![]() , which we will call a(ij), has a unique interpretation i
n terms of regression. The diagonal elements of
, which we will call a(ij), has a unique interpretation i
n terms of regression. The diagonal elements of ![]() , a(ii), are related to the multiple correlation between measure i as a criterion predicted from all other measures in the set, as follows:
, a(ii), are related to the multiple correlation between measure i as a criterion predicted from all other measures in the set, as follows:
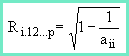 |
(1) |
Therefore, the diagonal elements allow us to easily compute the multiple correlation of each variable with all other variables in the set.
The off-diagonal elements are related to the beta weights of the regression equation where the criterion is equal to i (the row index) with each other variable j (the column index, in the following way:
 |
(2) |
where Beta is the weight for variable j as a predictor of criterion i, with all other variables partialled from j. Remember that Beta weights are directional, and the variance associated with other variables is partialled from the predictor (j), but n ot from the criterion (i).
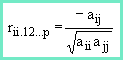
If we want the nondirectional partial correlation between any two variables i and j, controlling all other variables, we can also calculate that quantity from the off-diagonal element a(ij), as follows:
 |
(3) |
which is the partial correlation between i and j controlling all other variables.
Therefore, each element of the inverted correlation matrix is directly related to either a multiple correlation or a beta weight and partial correlation, which means that a great variety of useful information is tied up in the somewhat strange looking
numbers of ![]() .
.
To see why these things work out the way they do, let us compute the inverse of a 3x3 correlation matrix,
 |
Remember, the inverse equals the transpose of the cofactor matrix divided by the determinant. The determinant equals
|
|
(4) |
The cofactor matrix is calculated by replacing each element in the matrix with the determinant of what is left after removing both the row and column that the element occupies. Then every other value's sign is changed [(-1)i+j]. This results in the f ollowing cofactor matrix:
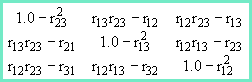 |
Consider Equation 3 above. If we reverse the sign of a(12), for example, we get the numerator of the partial correlation between variables 1 and 2, controlling 3. When divide by the square root of the product of the two diagonal elements, we complete the formula for a partial correlation,
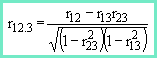 |
(5) |
Notice that in this case we do not have to worry about dividing by the determinant because it will cancel out.