| EENS 2110 |
Mineralogy |
| Tulane University |
Prof. Stephen A. Nelson |
|
TWO COMPONENT (BINARY) PHASE DIAGRAMS |
|
|
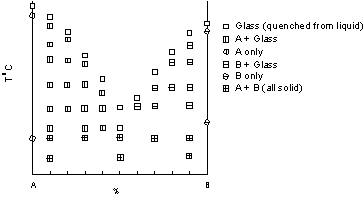
Experimental Determination of 2-Component Phase Diagrams As an example, we're going to look at how one might go about determining the stability of a mixture of 2 mineral phases, A and B. To perform these experiments we start with pure minerals A and B and then make mixtures in varying proportions. Each one of these mixtures, plus the pure A and pure B represent different compositions. In this case, we are only going to look at how the stability varies as with temperature and composition, holding Pressure constant at 1 atmosphere. This type of experiment can be done in a furnace with controlled temperature. Pressure does not have to be controlled because the phase relations will be determined at atmospheric pressure. The various compositions are placed in a capsule that will not react with any of the phases produced. Usually this would be Platinum. Each mixture is then placed in the furnace, the temperature is raised to some point and held at that temperature long enough for equilibrium between all of the phases to occur. The capsules are then quickly removed from the furnace and quenched rapidly. The rapid decrease in temperature that occurs during quenching helps to assure that no further reactions take place and the phase assemblage that was present at the higher temperature is preserved at room temperature. During quenching, any liquid that may have been present at high temperature is found to be glass. |
| After quenching, each capsule is opened and the phases present are determined using a microscope. In the example shown, we use different symbols to represent the mineral phase assemblages present for each composition run. In this set of experiments 6 different assemblages are found, and are plotted on a diagram with Temperature of the experiment plotted on the vertical axis, and composition in terms of %A or %B plotted on the horizontal axis. |  |
| Note that pure A plots at 100% A which corresponds to 0% B, and pure B
plots at 100%B, which corresponds to 0% A.
Note also that no experiments were run at temperatures higher than those where the first complete liquid appeared for each composition. |
| Once the points are plotted, we can then draw best-fit curves or lines between the data points to determine the Temperature - Composition stability fields for the various phase assemblages. These curves/lines are shown here, and the stability fields for each phase assemblage are labeled. the resulting phase diagram is called a binary eutectic diagram. Not all binary melting diagrams look like this, but this is the simplest and the type that we will discuss first. | 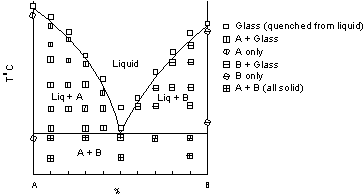 |
TWO COMPONENT EUTECTIC SYSTEMS Figure 1 shows the simplest of two component phase diagrams. The components are A and B, and the possible phases are pure crystals of A, pure crystals of B, and liquid with compositions ranging between pure A and pure B. Compositions are plotted across the bottom of the diagram. Note that composition can be expressed as either a percentage of A or a percentage of B, since the total percentage must add up to 100. (Compositions might also be expressed as mole fraction of A or B, in which case the total must add up to 1). Temperature or pressure is plotted on the vertical axis. For the case shown, we consider pressure to be constant, and therefore have plotted temperature on the vertical axis. |
| The curves separating the fields of A + Liquid from Liquid and B + Liquid from Liquid are termed liquidus curves. The horizontal line separating the fields of A + Liquid and B + Liquid from A + B all solid, is termed the solidus. The point, E, where the liquidus curves and solidus intersect, is termed the eutectic point. At the eutectic point in this two component system, all three phases, that is Liquid, crystals of A and crystals of B, all exist in equilibrium. Note that the eutectic is the only point on the diagram where this is true. | 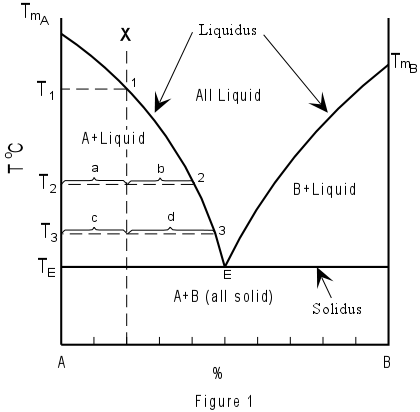 |
| Since we looking at a system at constant pressure, the phase rule in this case is F =
C +1 - P. The eutectic point is therefore an invariant point. If we change the
composition of the liquid or the temperature, the number of phases will be reduced to 2.
If the system contains only pure A, then the system is a one component system and phase A melts at only one temperature, the melting temperature of pure A, TmA. If the system contains only pure B, then it is a one component system and B melts only at the melting temperature of pure B, TmB. For all compositions between pure A and pure B, the melting temperature is drastically reduced, and melting begins at the eutectic temperature TE. Note that for all compositions between A and B the melting also occurs over a range of temperatures between the solidus and the liquidus. This is true for all compositions except one, that of the eutectic. The eutectic composition melts at only one temperature, TE. We will now consider the crystallization of a liquid with composition X in Figure 1. First, however, we must state the following rule, which must always be obeyed: Rule 1 - In equilibrium crystallization or melting in a closed system, the final composition of the system will be identical to the initial composition of the system. Therefore, according to rule 1, composition X, which is made up of a mixture of 80% A and 20% B, will have, as its final crystalline product a mixture of 80% crystals of A and 20% crystals of B. Composition X will be all liquid above the temperature T1, because it will lie in the field of all Liquid. If the temperature is lowered to T1, at T1 crystals of A begin to form. Further lowering of the temperature causes more crystals of A to form. As a result, the liquid composition must become more enriched in B as more crystals of A form out of the liquid. Thus, with lowering of temperature, the liquid composition will change from point 1 to point 2 to point 3 to point E as the temperature is lowered from T1 to T2 to T3 to TE respectively. At all temperatures between T1 and TE, two phases will be present in the system; liquid and crystals of A. At the eutectic temperature, TE, crystals of B will begin to form, and three phases will coexist; crystals of A, crystals of B, and liquid. The temperature must remain at TE until one of the phases disappears. Thus when the liquid crystallizes completely, only pure solid A and pure solid B will remain and mixture of these two solid phases will be in the proportions of the original mixture, that is 80% A and 20% B. The crystallization history of composition X can be written in abbreviated form as follows:
|
| If we were to stop the crystallization process at any point during crystallization and
observe how much of each phase is present we can use the following example to determine
what we would see.
For example, at a temperature T2 the amount of crystals of A and liquid (the only two phases present at this temperature) could be determined by measuring the distances a and b on figure 1. The percentages would then be given by the lever rule:
Note that since the amount of crystals must increase with falling temperature the proportional distance between the vertical line which marks the initial composition and the liquidus increases as temperature falls. Thus the distance used to calculate the amount of solid is always measured toward the liquid side of the initial composition. At the temperature T3, note that more crystals must have formed since the proportional distance d/(c+d) is greater than the proportional distance b/(a+b). Thus at T3 the lever rule gives:
At T3, note that the composition of the liquid is given at point 3, i.e. 53% A, the composition of the solid is pure A, and the composition of the system is still 80% A and 20% B. Make sure you understand the difference between composition of the phases and the amount or percentages of the phases. The melting process is exactly the reverse of the crystallization process. That is if we started with composition X at some temperature below TE the first liquid would form at TE. The temperature would remain constant at TE until all of the crystals of B were melted. The liquid composition would then change along the liquidus curve from E to point 1 as temperature increased until the temperature T1 was reached. Above T1 the system would contain only liquid with a composition of 80% A and 20% B. The melting process in abbreviated form is listed below:
|
INCONGRUENT MELTING Definition of terms: Liquidus - The line separating the field of all liquid from
that of liquid plus crystals. Solidus - The line separating the field of all solid from
that of liquid plus crystals. Eutectic point - the point on a phase diagram where the
maximum number of allowable phases are in equilibrium. When this point is reached, the
temperature must remain constant until one of the phases disappears. A eutectic is an
invariant point. Peritectic point - The point on a phase diagram where a
reaction takes place between a previously precipitated phase and the liquid to produce a
new solid phase. When this point is reached, the temperature must remain constant until
the reaction has run to completion. A peritectic is also an invariant point. Intermediate compound - A phase that has a composition
intermediate between two other phases. Congruent melting - melting wherein a phase melts to a liquid
with the same composition as the solid. Incongruent melting - melting wherein a phase melts to a
liquid with a composition different from the solid and produces a solid of different
composition to the original solid. For the case of incongruent melting, we will use the system forsterite (Mg2SiO4)
- silica (SiO2), which has an intermediate compound, enstatite (MgSiO3). This system is a prime example of the phenomena of incongruent melting in rocks, and
therefore gives insights into many aspects of mineral formation. A simplified version of the system forsterite - silica with its intermediate compound enstatite is shown in Figure 2. The crystallization histories for compositions X, Y, and Z will be documented in the following discussion. Each of these compositions behaves in a slightly different manner |
| Crystallization of Composition X | |
| Composition X is a mixture of 13 wt. % SiO2 and 87 wt. % Mg2SiO4.
Because this composition falls between the compositions of pure forsterite and pure
enstatite, it must end its crystallization history containing only crystals of forsterite
and enstatite. i.e. no quartz will occur in the final crystalline mixture.
If a mixture such as composition X is taken to a temperature above its liquidus (i.e. above 1800oC in Figure 2) it will be in an all liquid state. We now trace the cooling history of composition X. |
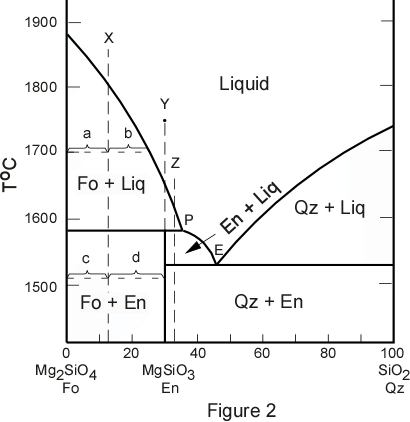 |
| As a liquid of composition X is cooled, nothing will happen until the temperature is
equal to the liquidus temperature at 1800o. At this point crystals of
forsterite (Fo) begin to precipitate out of the liquid. As the temperature is further
lowered, the composition of the liquid will change along the liquidus toward the
peritectic (P), and the crystals forming from the liquid will always be pure Fo until P is
reached.
At the temperature of the peritectic, about 1580o, note that three phases must be in equilibrium, Fo, liquid, and enstatite (En). At this point some of the crystals of Fo react with the liquid to produce crystals of En. The reaction that takes place can be written as follows:
(Where SiO2 in the reaction refers to the component of SiO2 in liquid with composition P). After all of the liquid is consumed by this reaction, only crystals of Fo and En will remain. The proportions of Fo and En in the final crystalline product can be found by applying the lever rule.
At any intermediate stage in the process, such as at 1700o the proportion of all phases present (Fo and liquid in this case) can similarly be found by applying the lever rule. at 1700oC
Note that melting of composition X is exactly the reverse of crystallization. Mixture X will begin to melt at the peritectic temperature. At this point En will melt to crystals of Fo plus liquid (incongruent melting). As soon as all of the En crystals have been consumed by this reaction, the temperature can be increased until it reaches 1800o at which point all of the Fo crystals will have been consumed and the only phase left will be liquid with a composition of the starting material. |
| Crystallization of Composition Y
Composition Y is equivalent to pure En. Thus only En may appear in the final crystalline product if perfect equilibrium is maintained. If composition Y is cooled from an all liquid state it first begins to crystallize at about 1650o. At 1650o crystals of Fo will begin to precipitate from the liquid. This will continue with further cooling until the temperature of the peritectic is reached. In this interval, the composition of the liquid must become more enriched in SiO2 and will thus change along the liquidus until it has the composition of the peritectic, P. At the peritectic temperature (1580o) all of the remaining liquid will react with all of the previously precipitated Fo to produce crystals of En. The temperature will remain constant until this reaction has gone to completion, after which the only phase present will be pure En. Thus, it can be seen that enstatite melts incongruently. If pure enstatite is heated to a temperature of 1580o it melts to Fo plus liquid. |
| Crystallization of Composition Z
Since composition Z lies between En and SiO2, it must end up with crystals of En and Qz (Quartz). If such a composition were cooled from some high temperature where it is in the all liquid state, it would remain all liquid until it reached the liquidus temperature at about 1600o. At this temperature crystals of Fo would begin to precipitate and the composition of the liquid would begin to change along the liquidus toward the peritectic, P. At P, all of the Fo previously precipitated would react with the liquid to produce crystals of En. After this reaction has run to completion, and all of the previously precipitated Fo is consumed, there would still remain some liquid. With decreasing temperature, more crystals of En would form, and the liquid composition would change along the liquidus toward the eutectic, E. At E crystals of Qz would begin to form, the temperature would remain constant until all of the liquid was used up, leaving crystals of Qz and En as the final solid. Note that because composition Z lies very close to the composition of pure En, the final crystalline product would consist mostly of En with a very small amount of Qz. For all compositions between P and 100% SiO2 the system would behave in an identical fashion to the simple Eutectic system discussed previously. |
| Fractional Crystallization in the System
Up to this point we have always been discussing the case of equilibrium crystallization. That is all solids remain in contact with the liquid until any reaction that takes place has run to completion. As is often the case in natural systems crystals can somehow become separated from the system so that they will not react at reaction points such as P. This is the case of fractional crystallization. Under fractional crystallization conditions the cooling and crystallization histories will be drastically different. In particular, the rule that the final composition must equal the initial composition will not be followed. As an example of this phenomena we will examine the fractional crystallization of composition X. Furthermore, we will look at the case of perfect fractional crystallization. During perfect fractional crystallization of composition X all of the Fo that is precipitated will be somehow removed from the system. (In nature this can occur by crystals sinking to the bottom of the liquid due to the fact that crystals generally tend to be more dense than liquids.) Note that if only some of the crystals are removed from the liquid we will have a case intermediate between perfect fractional crystallization and equilibrium crystallization. Cooling a liquid of composition X to the liquidus at 1800o will cause Fo to precipitate as before. With further cooling the liquid composition will change along the liquidus and more Fo will be precipitated. In this case, however, all of the Fo will be removed from the system as it crystallizes. Since the Fo is no longer present, the composition of the system will have the composition of the liquid (the Fo removed can no longer contribute to the composition of the system). Therefore, when the temperature reaches the peritectic temperature, 1580o, there will be no Fo available to react with the liquid, and the liquid (and system) will have a composition, P. Thus the liquid will now precipitate crystals of En and continue cooling to the eutectic, E, where crystals of Qz will form. The final crystalline product will consist of Qz and En. Compare this case with the previously discussed case of equilibrium crystallization of composition X. Note that under equilibrium conditions the final crystalline product of composition X contained crystals of Fo and En, while in the fractional crystallization case the final product contains En and Qz. Thus fractional crystallization has allowed an originally Fo rich composition to produce an SiO2 rich liquid and Qz appears in the final crystalline product. If you go back and look at simple eutectic systems, or look at fractional crystallization of composition Z in the more complex system, you should be able to see that fractional crystallization will have no effect on the phases produced in the final crystalline product, but will only change the proportions of the phases produced. Fractional crystallization is only effective in producing a different final phase assemblage if there is a reaction relationship of one of the phases to the liquid. |
SOLID SOLUTION SYSTEMS In the systems we've discussed so far, all of the mineral or solid phases have been pure phases, that is they have one and only one possible composition. This is not usually the case in nature, since substitution of one element for another often occurs due to the fact that some elements behave in a chemically similar fashion to other elements. When such substitutions occur, the phase can have a range of possible compositions, depending on the amount of substitution that takes place. Such solids that can have various amounts of elemental substitution are called solid solutions. A good example of a solid solution mineral is the mineral olivine. The general chemical formula for olivine is (Mg,Fe)2SiO4. Since Mg+2 and Fe+2 are about the same size and have the same charge, they may substitute for one another in the crystal structure of olivine. Thus olivine may have a composition anywhere between the pure Mg end member, forsterite (Mg2SiO4), and the pure Fe end member, fayalite (Fe2SiO4). When all compositions between two end members are possible, the solid solution is said to be a complete solid solution. Another good example of a complete solid solution is displayed in the plagioclase feldspars. In this case the solid solution is between the end members albite (NaAlSi3O8) and anorthite (CaAl2Si2O8). In order to maintain charge balance we cannot simply substitute Na+ for Ca+2, so this solid solution is what is called a coupled solid solution. In this case Na+Si+4 is substituted for Ca+2Al+3 in the plagioclase structure to produce intermediate compositions of plagioclase. Because the elements that substitute are not exactly the same size (they are similar in size) the amount of substitution is dependent on temperature and pressure and the solid solutions behave in a somewhat orderly fashion as illustrated below. Since plagioclase is one of the most common minerals in the earth's crust, we will discuss the phase diagram for the plagioclase system. The phase relations in the plagioclase system are shown in Figure 3 at constant pressure equal to that of the atmosphere (atmospheric pressure is 1 bar). In Figure 3 the upper curve is called the liquidus and the lower curve is called the solidus. At temperatures above the liquidus everything is liquid, below the solidus everything is solid (crystals of plagioclase solid solution). At temperatures between the solidus and liquidus crystals of plagioclase solid solution coexist in equilibrium with liquid. |
| Pure albite melts (or crystallizes) at 1118oC, and pure anorthite melts (or crystallizes) at 1500oC. Note that any composition of plagioclase between the two end members melts or crystallizes over a range of temperatures unlike the pure end members which have only one melting point. Thus we can read from the diagram that a solid solution containing 50% albite and 50% anorthite (Ab50An50) begins to melt at 1220o, point F, and the melting is complete at 1410o, point A. Inversely, if a melt of composition Ab50An50 is cooled it will begin to crystallize at 1410o and will be completely crystalline at 1220o. |
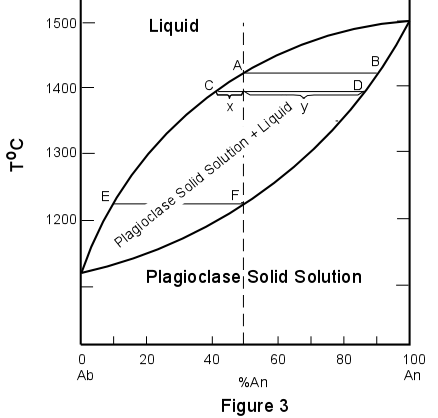 |
| We will now trace the crystallization history of composition X, which is Ab50An50.
Composition X is completely liquid above the liquidus (above 1410o). Cooling to
the liquidus at point A results in the crystallization of a small amount of plagioclase
solid solution. The composition of this plagioclase can be found by drawing an isotherm
(line of constant temperature, a horizontal line in this diagram) through the temperature
1410o. Where this isotherm intersects the solidus (at point B), the composition
of the solid can be found by drawing a vertical line to the base of the diagram. Thus it
is seen that the first crystals precipitated from composition X will have the composition
Ab10An90. Note that in this diagram crystals that are in equilibrium
with liquid will always be enriched in anorthite component relative to the liquid. As
crystallization continues with lowering of temperature the composition of the plagioclase
will change along the solidus, continually reacting with the liquid to produce crystals
more enriched in the Ab component. Meanwhile, the composition of the liquid will change
along the liquidus, thus also becoming more enriched in the Ab component. At a temperature
of 1395o the liquid composition will be at point C, while the solid composition
will be at point D. Crystallization proceeds until a temperature of about 1220o,
at which point the last remaining liquid will have a composition at E, and the solid will
have a composition equal to the original starting composition at point F.
At this point
all of the liquid will be consumed and the final crystalline product will have the
composition Ab50An50. |
| During crystallization the proportion of the solid continually increases while that of
the liquid continually decreases. Thus as the composition of the liquid becomes more
sodic, approaching E, its volume steadily decreases. Thus it can be seen that the amount
of liquid in equilibrium with the solid of composition F will be extremely small.
If at any point during the crystallization we wish to determine the amount of solid and liquid, we can apply the lever rule. As an example, we will determine the proportions of liquid and solid in the system at a temperature of 1395o. At this point, we measure the distances oC, oD, and CD. The percentages of liquid and solid are then given as follows:
The foregoing discussion assumes that equilibrium is maintained throughout the course of crystallization. This means that with falling temperature and continuing crystallization, the earlier-formed, more calcic crystals must react continuously with the liquid to produce homogeneous crystals that will become continuously more enriched in the sodic component. If this equilibrium cannot be maintained, then fractional crystallization will take place. We will distinguish between three contrasting conditions. |
|
EXSOLUTION Many minerals that show complete solid solution at higher temperatures do not show such
solid solution at lower temperatures. When this is the case, the phenomenon of exsolution
occurs. Since solid solutions are really one mineral phase dissolved in another mineral
phase to form a single mineral phase, exsolution implies that one or the other of the
mineral phases in the solution must "exsolve" or come out of solution with the
other mineral phase. |
| Figure 4 illustrates a phase diagram (much simplified) of the alkali feldspar system which exhibits such exsolution behavior at low temperatures. At high temperatures the diagram shows that albite (Ab) or NaAlSi3O8 and orthoclase (Or) or KAlSi3O8 form a complete solid solution series. This solid solution series is different from the plagioclase solid solution series only in that it has a minimum composition in the middle rather than at the composition of one of the pure end members. At temperatures just below the solidus, alkali feldspar solid solutions are stable. At lower temperatures, along the curve labeled "solvus" the solid solution is no longer stable. | 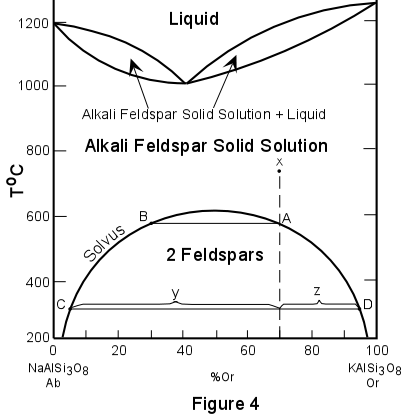 |
| In this case the exsolution phenomena occurs below the solidus and so is a "sub-solidus" reaction. In order to see what happens during exsolution we will examine what happens to a composition labeled X in Figure 4. We will start at a temperature of 750o in the region where alkali feldspar solid solutions are stable. At 750o the composition of the alkali feldspar solid solution is 70% orthoclase and 30% albite (Or70Ab30). |
| This solid solution remains stable with lowering of temperature until the temperature of the solvus is obtained at point A (a temperature of about 590o). At this temperature the solid solution is no longer stable and begins to exsolve. The composition of coexisting exsolved phases can be found by drawing an isotherm until it intersects the solvus. Such an isotherm at 590o shows that at this temperature a solid solution having the composition of point B (Or32Ab68) coexists with an alkali feldspar solid solution with the composition of point A (Or70Ab30). With further lowering of temperature further exsolution occurs. At a temperature of 300o our original composition X has exsolved into two alkali feldspar solid solutions, one with the composition of point C and one with a composition of point D. To find the relative proportions or percentages of each of the solid solutions, the lever rule can once again be applied. For example at 300o for composition X the percentage of the albite-rich solid solution is [z/(z+y)] x 100, while that of the orthoclase-rich solid solution is [y/(z+y)] x 100. With further lowering of temperature all of the albite and orthoclase in the two solid solutions could exsolve completely to produce a pure albite phase and a pure orthoclase phase. Such complete exsolution does occur in nature, but only if the temperature is lowered very slowly. Complete exsolution is only common in metamorphic rocks. More often, especially in granitic rocks, the two exsolved phases do not separate as individual crystals, but occur as intergrown crystals with exsolution lamellae of one crystal occurring within the other crystal. In the alkali feldspars containing such exsolution lamellae the result is to produce a texture called perthitic or perthite. Perthite on a microscopic scale is illustrated on page 540, figure 19.77 of your mineralogy text (Klein and Dutrow). |
Examples of Questions on this material that could be asked on an exam
|