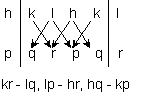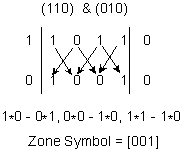Crystal Forms
As stated at the end of the last lecture, the next step is to use the Miller Index notation to designate crystal forms. A crystal form is a set of crystal faces that are related to each other by symmetry. To designate a crystal form (which could imply many faces) we use the Miller Index, or Miller-Bravais Index notation enclosing the indices in curly braces, i.e.
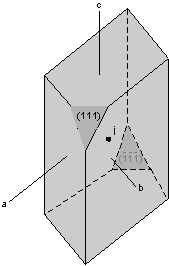
{101} or {11![]() 1}
1}
Such notation is called a form symbol.
An important point to note is that a form refers to a face or set of faces that have the same arrangement of atoms. Thus, the number of faces in a form depends on the symmetry of the crystal.
General Forms and Special Forms
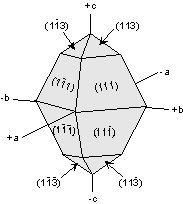
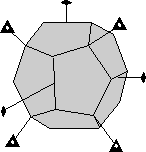
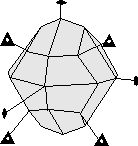
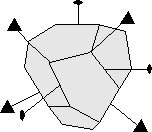
A general form is a form in a particular crystal class that contains faces that intersect all crystallographic axes at different lengths. It has the form symbol {hkl} All other forms that may be present are called special forms. In the monoclinic, triclinic, and orthorhombic crystal systems, the form {111} is a general form because in these systems faces of this form will intersect the a, b, and c axes at different lengths because the unit lengths are different on each axis. In crystals of higher symmetry, where two or more of the axes have equal length, a general form must intersect the equal length axes at different multiples of the unit length. Thus in the tetragonal system the form {121} is a general form. In the isometric system a general form would have to be something like {123}.
Open Forms and Closed Forms
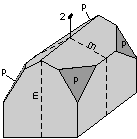
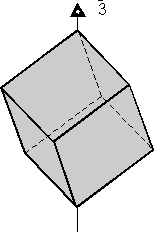
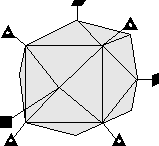
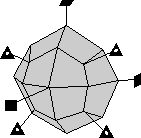
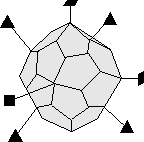
A closed form is a set of crystal faces that completely enclose space. Thus, in crystal classes that contain closed forms, a crystal can be made up of a single form.
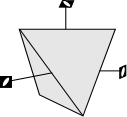
An open form is one or more crystal faces that do not completely enclose space.
- Example 1. Pedions are single faced forms. Since there
is only one face in the form a pedion cannot completely enclose
space. Thus, a crystal that has only pedions, must have at least
3 different pedions to completely enclose space.
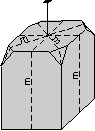
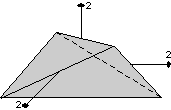
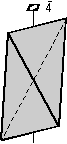
- Example 2. A prism is a 3 or more faced form wherein the
crystal faces are all parallel to the same line. If the faces
are all parallel then they cannot completely enclose space. Thus
crystals that have prisms must also have at least one additional form in
order to completely enclose space.
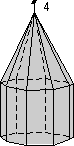
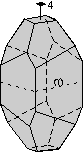
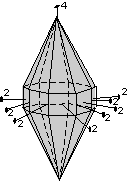
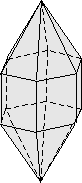
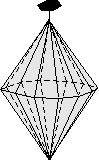
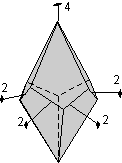
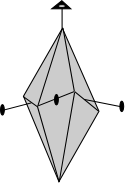
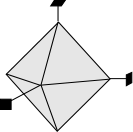
- Example 3. A dipyramid has at least 6 faces that meet in points at opposite ends of the crystal. These faces can completely enclose space, so a dipyramid is closed form. Although a crystal may be made up of a single dipyramid form, it may also have other forms present.
In your textbook on pages 139 to 142, forms 1 through 18 are open forms, while forms 19 through 48 are closed forms.
There are 48 possible forms that can be developed as the result of the 32 combinations of symmetry. We here discuss some, but not all of these forms.