* biological catalyst which speeds up rate of chemical reactions
* specific for particular substrates
* can regulate reactions by responding to signals from surroundings
* usually made of protein, but some RNA molecules also can act as catalysts
* study of reaction rates
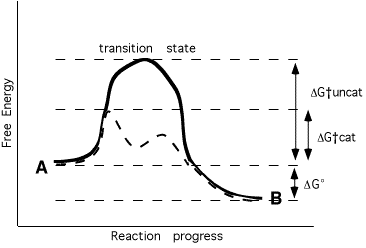
rate of any chemical reaction limited by energy needed to reach transition state
equilibrium ratio of A/B dependent on relative free energy of A and B (not changed by enzyme)
Enzyme speeds up rate of reaction:
* stabilizes transition state - lower energy required to achieve it
* also:
* entropy reduction - reduces disorder by orienting substrates for reaction
* covalent catalysis - may form covalent bond to substrate during reaction
--> new pathway of reaction with lower activation energy (also important
for reaction coupling)
* may bind metal of other cofactor that does work of reaction (Mg++)
Enzyme binds reactants (substrates - S) at active site
* active site typically a small portion of the volume of the enzyme,
* rest of enzyme necessary for structural stability, proper folding, also
may have regulatory domains
Substrate bound through series of weak interactions:
Hbonds, VDW, hydrophobics
--> specificity (substrate missing any key feature is not bound efficiently)
How does S fit E? Lock-and-key? Actually more of an induced fit, enzyme changes conformation upon binding substrate
An example of an enzyme:
Chymotrypsin-
* a serine protease (i. e. has serine at active site)
* digests proteins at C-term side of Y, W or F residues
* important active site residues: Asp(D)102, His(H)57 and Ser(S)195.
* Uses stabilization of transition state, entropy reduction, and covalent
catalysis to enhance reaction rate
rate of uncatalyzed reaction: 10-10/sec
rate of uncatalyzed reaction: 102/sec
rate enhancement of: 1012/sec!
Serine Protease Mechanism
(modified from Garrett and Grisham, p441)
Enzyme binds substrate, orienting it for subsequent reaction. (Reduction of entropy)
His57 accepts proton from ser195, allowing O of ser to attack C=O carbon of substrate. Protonated his stabilized by negative charge of neighboring asp102
Tetrahedral transition state intermediate formed, stabilized by H-bonds from backbone NH protons of residues 193 and 195. Enzyme is covalently linked to substrate. Peptide N of substrate accepts proton from his57.
Electrons move from C-N bond to +-charged N, breaking C-N bond of substrate. C=O bond reformed.
Amino fragment of substrate released, carboxyl fragment remains covalently bound to ser195 as acyl-enzyme intermediate.
His57 accepts proton from solvent H2O, remaining OH attacks C=O carbon of acyl-enzyme intermediate.
Tetrahedral transition state formed again, stabilized by H-bonds (not shown this time). Subsequently, acyl bond breaks, proton transferrred from his57 to ser195, C=O bond reformed on product.
Carboxyl proton lost.
C-terminal product released.
Measuring rate of enzyme catalysis - enzyme kinetics
(early in reaction [P]<<[S])
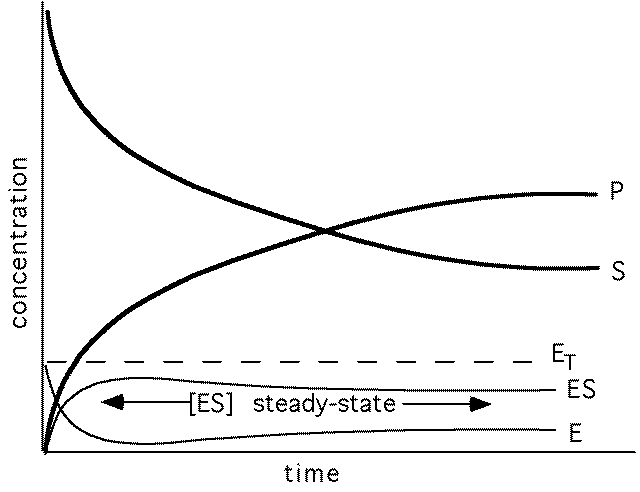
S=substrate, P=product, E= free enzyme, ES=enzyme-substrate complex ET=total enzyme
[ES] ~ constant : steady state
Varying the substrate concentration changes the rate of reaction:
The rate of product formation, V:
V = k3 [ES]
and the maximum reaction rate, Vmax , occurs when all enzyme is bound
to substrate:
Vmax = k3 [ET]
Under steady-state conditions:
rate of ES formation =rate of ES breakdown
[E][S]k1 = [ES]k2+[ES]k3
or:
[E][S]k1 = [ES] (k2+ k3)
solving for [ES]:
since k1,k2, and k3 should be constant for a particular E and S, we'll define a constant KM , based upon them:

substituting into the previous equation:
we don't really know [E] or [ES], but:
[E]=[ET]-[ES]
substituting for [E]:
factoring:
[ET] [S]-[ES][S] = [ES]KM
rearranging:
[ET] [S] = [ES][S] + KM [ES]
factoring:
[ET] [S] = [ES] ([S] + KM )
dividing both sides by ([S] + KM ):
now substitute this into the equation for reaction velocity:
V = k3 [ES]:
when the enzyme is fully saturated, velocity reaches Vmax
:
Vmax = k3 [ET]
substituting again:
This is the Michaelis-Menten equation.
what happens when [S] = KM ?
or:
V = Vmax /2
Reaction velocity is one-half of Vmax when [S] = KM
.
But it is hard to determine Vmax and KM from this
type of graph. How do you actually determine Vmax and KM
?
You can use a computer graphing program to fit the data to a curve.
Or you can rearrange the Michaelis-Menten equation to make it easier to
plot and determine Vmax and KM.
Start with the Michaelis-Menten equation:
take the inverse of both sides:
factor:
which can be rewritten as:
compare to the plot of a linear equation:
So plotting 1/S for x and 1/V for y yields a straight
line with 1/ Vmax for the y-intercept (b). The slope
(m) = KM / Vmax and the x-intercept= -1/ KM
.
This is the Lineweaver-Burk plot:
In vivo often [S] ~ KM:
if [S] = 1000 KM, rate still only 2X higher than when [S] =
KM (waste of S; reaction rate is insensitive to [S])
if [S] = KM /1000, most of E unoccupied (waste of E)
Knowing KM useful for setting up reactions in lab:
eg. picking a DNA polymerase for 32P labeling (expensive, dangerous
in large quantities)
E. coli polI KM for dNTPs ~1uM
AMV reverse transcriptase KM ~1mM
So polI can more efficiently incorporate small [ ] of dNTP
polI formerly used for DNA sequencing, but KM varies for each
dNTP and ddNTP, so optimizing reaction was quite tedious. T7, Taq polymerase:
similar KM for all dNTP and ddNTPs easier to optimize
k3 (kcat for multistep reaction)
Vmax = k3 [ET]
k3= reactions catalyzed/mol enzyme-sec
each reaction requires 1/ k3 sec to occur
carbonic anhydrase: k3 =6X105/s time per reaction =1.7 us
chymotrypsin: kcat =1X102/s time per reaction =0.01 s
ribonuclease P =0.2/s time per reaction =5 s
kcat/ KM
when [S] << KM
so V is dependent upon kcat/ KM at a given [ET] [S].
Can compare affinities for different substrates using low [S]:
Chymotrypsin:
| AA at cleavage site | kcat/ KM |
| glycine | 1.3X10-1 |
| phenylalanine | 1X105 |
showing preference for bulky hydrophobics at active site.
if k3>> k2
k1 limited by diffusion of S to E: 108 -109 /M-sec
"catalytic perfection" production of product limited by rate of encountering substrate in solution.
carbonic anhydrase, acetyl cholinesterase - ~ catalytically perfect, kcat/ KM around 108 /M-sec
Even this limit can be surpassed by enzymatic assemblies - related enzymes co-localized, product of one E released to next to use as S. Faster than diffusion.
Multicomponent reactions
Most reactions more complex than
such as:
Kinetics also become much more complicated
Do reactants bind to enzyme at same time? (ternary complex formation)
Do reactants bind in particular order?
Random binding order:
ordered binding
Ping-pong Bi-Bi:
Equations can get pretty hairy, usually keep one [S] constant and high, vary the other to determine kinetic parameters.
Inhibitors
Specific compounds that slow enzymatic reactions
Very important tool for studying reaction components
Major types of competitors:
Competitive inhibitors:
Usually resemble substrate (including product)
Inhibitor (I) binds to active site instead of substrate
Vmax not changed, just requires more S to reach it. Apparent KM , KMAPP goes up.
Noncompetitive inhibition
I and S bind to different sites, but only ES --> P
KM not affected, but Vmax is decreased.