|
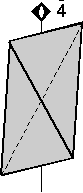
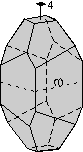
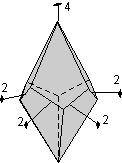
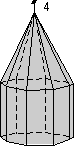
The 32 Crystal Classes
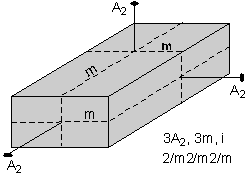
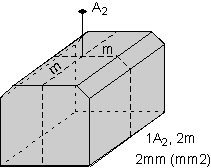
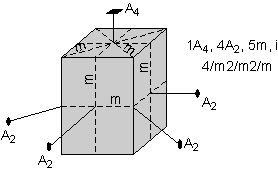
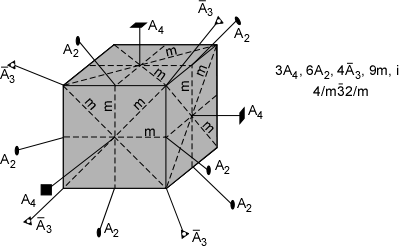
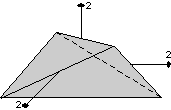
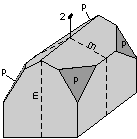
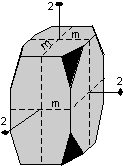
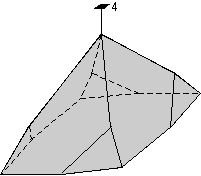
The 32 crystal classes represent the 32 possible combinations of
symmetry operations. Each crystal class will have crystal faces that
uniquely define the symmetry of the class. These faces, or groups of
faces are called crystal forms. Note that you are not expected to
memorize the crystal classes, their names, or the symmetry associated with
each class. You will, however, be expected to determine the symmetry
content of crystal models, after which you can consult the tables in your
textbook, lab handouts, or lecture notes. All testing on this
material in the lab will be open book.
In this lecture we will go over some of the crystal classes and their
symmetry. I will not be able to cover all of the 32 classes.
You will, however, see many of the 32 classes during your lab work. Note that it is not easy to draw a
crystal of some classes without
adding more symmetry or that can be easily seen in a two dimensional
drawing.
The table below shows the 32 crystal classes, their symmetry,
Hermann-Mauguin symbol, and class name.
|