
tan 45o = 1b/1a
then
1a/1b = 1/tan 45o= 1
So, a/b: b/b = 1: 1
| EENS 2110 |
Mineralogy |
| Tulane University |
Prof. Stephen A. Nelson |
|
Crystallographic Calculations |
|
|
|
|
Crystallographic Calculations Crystallographic calculations involve the following:
Most of what you will do in lab or on exams will involve crystallographic calculations in the orthorhombic, tetragonal, hexagonal, or isometric systems, where the axes angles are fixed. Note that you will always be given enough information to solve the problem. Some of the problems you might be expected to solve involve determination of Miller Indices from the ρ and φ angles, to determine the ρ and φ angles for faces of mineral with known axial ratios, or to determine axial ratios of minerals that have faces of known ρ and φ angles. First let's review some of the things we know about Miller indices and ρ and φ angles. In the orthorhombic, tetragonal, or isometric systems.
So, φ = 0o or φ = 180o
So, φ = 90o or φ = 270o
So, ρ = 90o and φ = 0o or φ = 180o.
Now let's do some examples |
|
|
For the (110) we note that it does not intersect the c axis, so we can look at it in the two dimensional plane containing the a and b axes, as shown in the drawing below. From this face we should be able to determine the a/b axial ratio. Since the φ angle is the angle between the normal to the face and the b axis, by similar triangles we know that the φ angle also occurs between the a axis and the face.
|
|
|
Thus, we can write:
tan 45o = 1b/1a then
1a/1b = 1/tan 45o= 1
So, a/b: b/b = 1: 1 |
|
We next note that the (011) intersects the b and c axes
only, so we can examine this face in the plane containing only b
and c, as shown below. From this drawing we can obtain the
c/b axial ratio. Since the ρ angle is
the angle between the pole to the face and the c axis, again by similar
triangles we know that the ρ angle also
occurs between the b axis and the (011) face. |
|
|
Thus, we can write:
tan 70o = 1c/1b then
c/b = arctan 70o
So, c/b = 2.7475 |
|
so, a : b : c = 1 : 1 : 2.7475 and the mineral must be tetragonal, since a/b =1. |
|
|
Faces ρ φ (120) 90o 70o (011) 32o 0o The face (120) does not intersect the c axis, so we can look at this face in the plane containing only the a and b axes. We must also remember that Miller Indices represent the inverse of the intercepts, so the face (120) intersects the a axis at twice the number of unit lengths that it intersects the b axis. Since the φ angle is the angle between the normal to the face and the b axis, by similar triangles we know that the φ angle also occurs between the a axis and the (120) face. |
|
|
Then we can write: tan 70o = 1b/2a
a/b = 1/2tan70o 1a/1b = 0.18199 |
|
We next note that the (011) intersects the b and c axes only, so we can examine this face in the plane containing only b and c, as shown below. From this drawing we can obtain the c/b axial ratio. Since the ρ angle is the angle between the face and the c axis, again by similar triangles we know that the ρ angle also occurs between the b axis and the (011) face. |
|
|
For this face we can determine that
tan 32o = 1c/1b
1c/1b = 0.6248 |
|
|
|
|
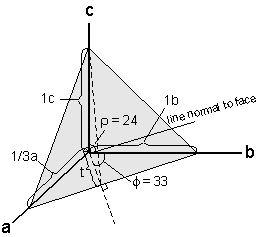
c. Faces ρ φ(311) 24o 33o
|
|
We first attempt to draw a 3-dimensional view of this face.
Notice that the φ angle is
measured in the horizontal plane that includes the a and b
axes. The ρ angle is measured in a vertical
plane that includes the c axis and the line normal to the face in
the a - b horizontal plane, and is measured between the c
axis and a line normal to the face. |
 |
|
|
We can determine the a/b part of the axial ratio by looking at the projection of this face in the a - b plane. 1b/(1/3)a = tan 33o |
|
In order to determine the length of the c axis, we need to know the length of the line labeled t, because this line forms the base of the triangle in which the ρ angle is measured. The length of the line t is:
t/b = cos 33o |
|
|
We can now use this to determine the c/b axial ratio. 1c/t = tan 24o c/b = 0.3747 |
|
Thus, the axial ratio for this mineral is 4.6196 : 1 : 0.3747 |
|
|
Now we'll look at an example where we are given the axial ratio of the mineral and asked to calculate the ρ and φ angles for the faces.
|
|
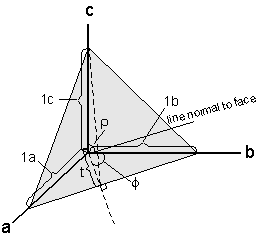
In this case the intercept on the all three axes is 1. |
 |
|
|
Since the φ angle for this face is measured in the horizontal a - b plane, we can draw the plane containing only the a and b axes to determine the angle. Since the axial ratio tells us that the relative lengths of the a and b axes are equal tan φ = 1b/1b = 1 φ = 45o |
|
t/b = cos 45o |
|
|
Now we can determine the angle by drawing the plane that includes the c axis and the line t. In this plane we can let the length of the c = 5b, from the axial ratio. Then: tan ρ = 5b/t tan ρ = 5b/0.7071b tan ρ = 5/0.7071 tan ρ = 7.071 ρ = arctan (7.071) = 81.95o |
|
So for the (111) face in this crystal ρ =81.95o and φ = 45o.
|
|
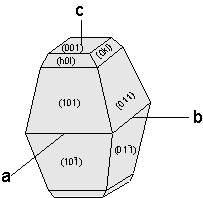
For the face (101)
|
 |
|
|
tan so, tan 70o = c/a = 2.7475 and the axial ratio is: 1 :1 : 2.7475 |
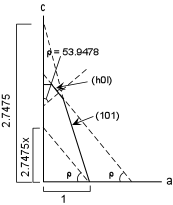 |
tan (53.9478) = 2.7475x/1, and thus, x = 0.5 The parameters for this face are then: 1,
|
Since the mineral is tetragonal, the face labeled (0hl) would have the Miller Index (012). Problems such as these could be asked on any laboratory exam. |