EENS 2110

Mineralogy
Tulane University

Prof. Stephen A. Nelson

Crystal Morphology, Crystal Symmetry, Crystallographic Axes

Crystal Morphology and Crystal Symmetry

 

The symmetry observed in crystals as exhibited by their crystal faces is due to the ordered internal arrangement of atoms in a crystal structure, as mentioned previously.  This arrangement of atoms in crystals is called a lattice.  
In 2-dimensions a plane lattice consists of an orderly array of points. The array is defined by the spacing between points and the directions (or angles) between the points.  Thus, the array can be reproduced by specifying the distance and angle to move from point to point.  This is referred to as translational symmetry.  In the example here, the array is reproduced by moving down a distance a and moving to the right a distance b.  The angle between the two directions of translation in this case is 90o

In the example to the right, the translation distances a and b are not equal and the translation angle is not 90o.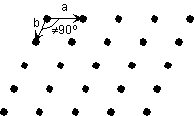

 

Crystals, of course, are made up of 3-dimensional arrays of atoms.  Such 3-dimensional arrays are called space lattices.  We discuss these space lattices in 3-dimensions in much more detail later.  For now, however, we will continue to look a plane lattices and note that everything that applies to these 2-dimensional lattice also applies to space lattices.

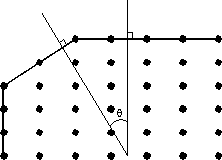
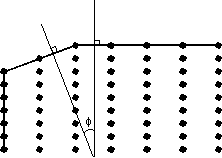
There are four important points about crystal lattices that are noteworthy for our study of crystals:

  1. Crystal faces develop along planes defined by the points in the lattice.  In other words, all crystal faces must intersect atoms or molecules that make up the points.   A face is more commonly developed in a crystal if it intersects a larger number of lattice points.  This is known as the Bravais Law.

For example, in the plane lattice shown at the right, faces will be more common if they develop along the lattice planes labeled 1, somewhat common if they develop along those labeled 2, and less and less common if they develop along planes labeled 3, 4, and 5.
  1. The angle between crystal faces is controlled by the spacing between lattice points.

As you can see from the imaginary 2-dimensional crystal lattice shown here, the angle q between the face that runs diagonally across the lattice and the horizontal face will depend on the spacing between the lattice points.  Note that angles between faces are measured as the angle between the normals (lines perpendicular) to the faces.  This applies in 3-dimesions as well.

Changing the lattice spacing changes the angular relationship.  The lattice shown here has the same horizontal spacing between lattice points, but a smaller vertical spacing.  Note how the angle f between the diagonal face and the horizontal face in this example is smaller than in the previous example.
  1. Since all crystals of the same substance will have the same spacing between lattice points (they have the same crystal structure), the angles between corresponding faces of the same mineral will be the same.  This is known as the Law of constancy of interfacial angles, as discussed previously.
  1. The symmetry of the lattice will determine the angular relationships between crystal faces.  Thus, in imperfect crystals or distorted crystals where the lengths of the edges or faces of symmetry related faces are not equal, the symmetry can still be determined by the angles between the faces.

    In the example shown here, the upper diagram shows a perfect crystal with the symmetrically related faces have equal lengths.  The low diagram shows a crystal built on the same lattice, but with distorted faces.  Note that the angles between faces in the distorted crystal are the same as in the perfect crystal.
In order to know which faces on different crystals are the corresponding faces, we need some kind of standard coordinate system onto which we can orient the crystals and thus be able to refer to different directions and different planes within the crystals.  Such a coordinate system is based on the concept of the crystallographic axes.


Crystallographic Axes

The crystallographic axes are imaginary lines that we can draw within the crystal lattice.  These will define a coordinate system within the crystal.  For 3-dimensional space lattices we need 3 or in some cases 4 crystallographic axes that define directions within the crystal lattices.  Depending on the symmetry of the lattice, the directions may or may not be perpendicular to one another, and the divisions along the coordinate axes may or may not be equal along the axes.  As we will see later, the lengths of the axes are in some way proportional to the lattice spacing along an axis and this is defined by the smallest group of points necessary to allow for translational symmetry to reproduce the lattice.

We here discuss the basic concepts of the crystallographic axes.  As we will see, the axes are defined based on the symmetry of the lattice and the crystal.  Each crystal system has different conventions that define the orientation of the axes, and the relative lengths of the axes.

 

Unit Cells

The "lengths" of the various crystallographic axes are defined on the basis of the unit cell.  When arrays of atoms or molecules are laid out in a space lattice we define a group of such atoms as the unit cell.  This unit cell contains all the necessary points on the lattice that can be translated to repeat itself in an infinite array.  In other words, the unit cell defines the basic building blocks of the crystal, and the entire crystal is made up of repeatedly translated unit cells.
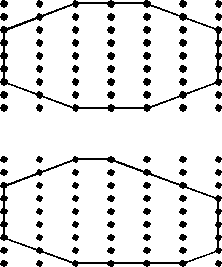
In defining a unit cell for a crystal the choice is somewhat arbitrary.  But, the best choice is one where:
  1. The edges of the unit cell should coincide with the symmetry of the lattice.
  2. The edges of the unit cell should be related by the symmetry of the lattice.
  3. The smallest possible cell that contains all elements should be chosen. 

For example, in the 2-dimensional lattice shown here there are 6 possible choices to define the unit cell, labeled a through f.  The lattice has 2-fold rotational symmetry about an axis perpendicular to the page.  Since the lattice itself does not have 3-fold or 6-fold rotational symmetry, choices a and b would not  be wise choices for the unit cell.  Choice f can be eliminated because it is really just half of cell b.  The edges of  c and e are not coincident or parallel to any 2-fold axes that lie in the plane of the page.  Thus our best choice would cell d. 
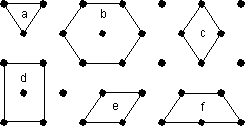Once we have chosen a unit cell for the crystal, then it can be oriented on the crystallographic axes to define the angles between the axes and to define the axial lengths.  This will allow us to define directions within the crystal that become important when we realize that many properties of crystals depend on direction in the crystal.  Properties that depend on direction in the crystal are called vectorial properties.  We'll discuss these in a later lecture.

Another important point is that the relative lengths of the crystallographic axes, or unit cell edges, can be determined from measurements of the angles between crystal faces.  We will consider measurements of axial lengths, and develop a system to define directions and label crystal faces in the next lecture.

Examples of questions on this material that could be asked on an exam

  1. Define the following:  (a) Bravais Law, (b) Law of constancy of interfacial angles, (c) unit cell, (d) vectorial properties of crystals.

  2. How are the crystallographic axes detemined in each of the 6 crystal classes.

  3. Explain why the spacing of lattice points and symmetry of the crystal lattice determine the angles between crystal faces.

Return to EENS 2110 Page