EENS 2110

Mineralogy
Tulane University

Prof. Stephen A. Nelson

Introduction and Symmetry Operations

 

Mineralogy

Definition of a Mineral

A mineral is a naturally occurring homogeneous solid with a definite (but not generally fixed) chemical composition and a highly ordered atomic arrangement, usually formed by an inorganic process.

  • Naturally Occurring - Means it forms by itself in nature.  Human made minerals are referred to as synthetic minerals.

  • Homogeneous - means that it is a compound that contains the same chemical composition throughout, and cannot by physically separated into more than 1 chemical compound.

  • Solid - means that it not a gas, liquid, or plasma.

  • Definite chemical composition - means that the chemical composition can be expressed by a chemical formula.  Examples:

    • Quartz has the chemical formula SiO2.  Whenever we find quartz it consists of Si and O in a ratio of 1 Si to 2 O atoms.

    • Olivine is an example of a mineral that does not have a fixed chemical composition.  In nature we find that Mg and Fe atoms have the same size and charge and therefore can easily substitute for one another in a mineral.  Thus, olivine can have the chemical formula Mg2SiO4 or Fe2SiO4 or anything in between.  This is usually expressed with a formula indicating the possible substitution - (Mg,Fe)2SiO4.

  • Highly ordered atomic arrangement - means that the atoms in a mineral are arranged in an ordered geometric pattern.  This ordered arrangement of atoms is called a crystal structure, and thus all minerals are crystals.  For each mineral has a crystal structure that will always be found for that mineral, i.e. every crystal of quartz will have the same ordered internal arrangement of atoms.  If the crystal structure is different, then we give the mineral a different name.  A solid compound that meets the other criteria, but has not definite crystal structure is a said to be amorphous. 

One of the consequences of this ordered internal arrangement of atoms is that all crystals of the same mineral look similar.  This was discovered by Nicolas Steno in 1669 and is expressed as Steno's Law of constancy of interfacial angles - angles between corresponding crystal faces of the same mineral have the same angle. This is true even if the crystals are distorted as illustrated by the cross-sections through 3 quartz crystals shown below.

 

 

Another consequence is that since the ordered arrangement of atoms shows symmetry, perfectly formed crystals also show a symmetrical arrangement of crystal faces, since the location of the faces is controlled by the arrangement of atoms in the crystal structure.

  • Usually formed by an inorganic process - The traditional definition of a mineral excluded those compounds formed by organic processes, but this eliminates a large number of minerals that are formed by living organisms, in particular many of the carbonate and phosphate minerals that make up the shells and bones of living organisms.  Thus, a better definition appends "usually" to the formed by inorganic processes.  The best definition, however, should probably make no restrictions on how the mineral forms. 

Symmetry

Crystals, and therefore minerals, have an ordered internal arrangement of atoms.  This ordered arrangement shows symmetry, i.e. the atoms are arranged in a symmetrical fashion on a three dimensional network referred to as a lattice.  When a crystal forms in an environment where there are no impediments to its growth, crystal faces form as smooth planar boundaries that make up the surface of the crystal.  These crystal faces reflect the ordered internal arrangement of atoms and thus reflect the symmetry of the crystal lattice.  To see this, let's first imagine a small 2 dimensional crystal composed of atoms in an ordered internal arrangement as shown below.  Although all of the atoms in this lattice are the same, I have colored one of them gray so we can keep track of its position.

 
If we rotate the simple crystals by 90o notice that the lattice and crystal look exactly the same as what we started with.  Rotate it another 90o and again its the same.  Another 90o rotation again results in an identical crystal, and another 90o rotation returns the crystal to its original orientation.  Thus, in 1 360o rotation, the crystal has repeated itself, or looks identical 4 times.  We thus say that this object has 4-fold rotational symmetry.


Symmetry Operations and Elements

A Symmetry operation is an operation that can be performed either physically or imaginatively that results in no change in the appearance of an object.  Again it is emphasized that in crystals, the symmetry is internal, that is it is an ordered geometrical arrangement of atoms and molecules on the crystal lattice.  But, since the internal symmetry is reflected in the external form of perfect crystals, we are going to concentrate on external symmetry, because this is what we can observe. 

There are 3 types of symmetry operations: rotation, reflection, and inversion.  We will look at each of these in turn.

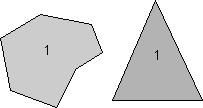
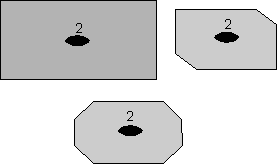
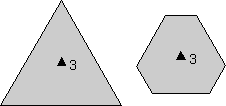
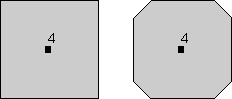
Rotational Symmetry

As illustrated above, if an object can be rotated about an axis and repeats itself every 90o of rotation then it is said to have an axis of 4-fold rotational symmetry.  The axis along which the rotation is performed is an element of symmetry referred to as a rotation axis.   The following types of rotational symmetry axes are possible in crystals.
  • 1-Fold Rotation Axis - An object that requires rotation of a full 360o in order to restore it to its original appearance has no rotational symmetry.  Since it repeats itself 1 time every 360o it is said to have a 1-fold axis of rotational symmetry.

 
  • 2-fold Rotation Axis - If an object appears identical after a rotation of 180o, that is twice in a 360o rotation, then it is said to have a 2-fold rotation axis (360/180 = 2).  Note that in these examples the axes we are referring to are imaginary lines that extend toward you perpendicular to the page or blackboard.  A filled oval shape represents the point where the 2-fold rotation axis intersects the page.  

This symbolism will be used for a 2-fold rotation axis throughout the lectures and in your text.
  • 3-Fold Rotation Axis- Objects that repeat themselves upon rotation of 120o are said to have a 3-fold axis of rotational symmetry (360/120 =3), and they will repeat 3 times in a 360o rotation.  A filled triangle is used to symbolize the location of 3-fold rotation axis.
 
  • 4-Fold Rotation Axis  - If an object repeats itself after 90o of rotation, it will repeat 4 times in a 360o rotation, as illustrated previously.  A filled square is used to symbolize the location of 4-fold axis of rotational symmetry.
  • 6-Fold Rotation Axis - If rotation of 60o about an axis causes the object to repeat itself, then it has 6-fold axis of rotational symmetry (360/60=6).  A  filled hexagon is used as the symbol for a 6-fold rotation axis. 

 

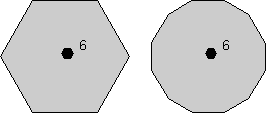Although objects themselves may appear to have 5-fold, 7-fold, 8-fold, or higher-fold rotation axes, these are not possible in crystals.  The reason is that the external shape of a crystal is based on a geometric arrangement of atoms.  Note that if we try to combine objects with 5-fold and 8-fold apparent symmetry, that we cannot combine them in such a way that they completely fill space, as illustrated below.

Mirror Symmetry

A mirror symmetry operation is an imaginary operation that can be performed to reproduce an object.  The operation is done by imagining that you cut the object in half, then place a mirror next to one of the halves of the object along the cut.  If the reflection in the mirror reproduces the other half of the object, then the object is said to have mirror symmetry.  The plane of the mirror is an element of symmetry referred to as a mirror plane, and is symbolized with the letter m.  As an example, the human body is an object that approximates mirror symmetry, with the mirror plane cutting through the center of the head, the center of nose and down to the groin.

The rectangles shown below  have two planes of mirror symmetry.

 
The rectangle on the left has a mirror plane that runs vertically on the page and is perpendicular to the page.  The rectangle on the right has a mirror plane that runs horizontally and is perpendicular to the page.  The dashed parts of the rectangles below show the part the rectangles that would be seen as a reflection in the mirror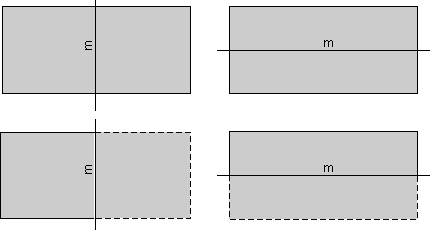
The rectangles shown above have two planes of mirror symmetry.  Three dimensional and more complex objects could have more.  For example, the hexagon shown above, not only has a 6-fold rotation axis, but has 6 mirror planes.

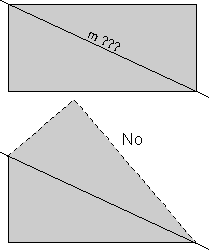
Note that a rectangle does not have mirror symmetry along the diagonal lines.  If we cut the rectangle along a diagonal such as that labeled  "m ???", as shown in the upper diagram, reflected the lower half in the mirror, then we would see what is shown by the dashed lines in lower diagram.  Since this does not reproduce the original rectangle, the line "m???" does not represent a mirror plane.

 

 

Center of Symmetry

Another operation that can be performed is inversion through a point.  In this operation lines are drawn from all points on the object through a point in the center of the object, called a symmetry center (symbolized with the letter "i"). The lines each have lengths that are equidistant from the original points.  When the ends of the lines are connected, the original object is reproduced inverted from its original appearance.  In the diagram shown here, only a few such lines are drawn for the small triangular face. The right hand diagram shows the object without the imaginary lines that reproduced the object.  
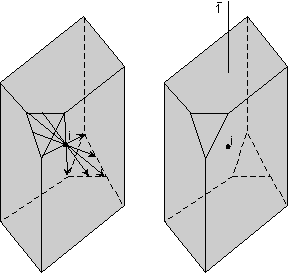If an object has only a center of symmetry, we say that it has a 1 fold rotoinversion axis.  Such an axis has the symbol , as shown in the right hand diagram above.  Note that crystals that have a center of symmetry will exhibit the property that if you place it on a table there will be a face on the top of the crystal that will be parallel to the surface of the table and identical to the face resting on the table.

 

Rotoinversion

Combinations of rotation with a center of symmetry perform the symmetry operation of rotoinversion.  Objects that have rotoinversion symmetry have an element of symmetry called a rotoinversion axis.  A 1-fold rotoinversion axis is the same as a center of symmetry, as discussed above.  Other possible rotoinversion are as follows:
 
  • 2-fold Rotoinversion - The operation of 2-fold rotoinversion involves first rotating the object by 180o then inverting it through an inversion center.  This operation is equivalent to having a mirror plane perpendicular to the 2-fold rotoinversion axis.  A 2-fold rotoinversion axis is symbolized as a 2 with a bar over the top, and would be pronounced as "bar 2".  But, since this the equivalent of a mirror plane, m, the bar 2 is rarely used.
  • 3-fold Rotoinversion - This involves rotating the object by 120o (360/3 = 120), and inverting through a center.  A cube is good example of an object that possesses 3-fold rotoinversion axes.  A 3-fold rotoinversion axis is denoted as (pronounced "bar 3").  Note that there are actually four axes in a cube, one running through each of the corners of the cube. If one holds one of the axes vertical, then note that there are 3 faces on top, and 3 identical faces upside down on the bottom that are offset from the top faces by 120o.  
  • 4-fold Rotoinversion - This involves rotation of the object by 90o then inverting through a center.  A four fold rotoinversion axis is symbolized as .  Note that an object possessing a 4- fold rotoinversion axis will have two faces on top and two identical faces upside down on the bottom, if the axis is held in the vertical position.
  • 6-fold Rotoinversion - A 6-fold rotoinversion axis () involves rotating the object by 60o and inverting through a center.  Note that this operation is identical to having the combination of a 3-fold rotation axis perpendicular to a mirror plane.  

 

 

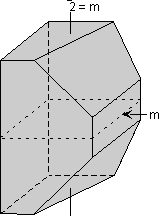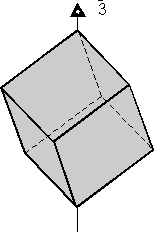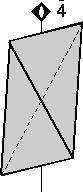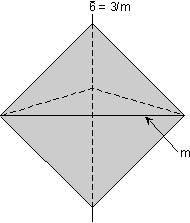Combinations of Symmetry Operations

As should be evident by now, in three dimensional objects, such as crystals, symmetry elements may be present in several different combinations.  In fact, in crystals there are 32 possible combinations of symmetry elements.  These 32 combinations define the 32 Crystal Classes.  Every crystal must belong to one of these 32 crystal classes.  In the next lecture we will start to go over each of these crystal classes in detail, but the best way to be able to identify each crystal class is not by listening to me lecture, not necessarily by reading about each class, but actually looking at models of perfect crystals in the lab.  In fact, it is my opinion that it is next to impossible to identify symmetry elements and crystal classes without spending a lot of time examining and studying the 3-dimensional models in lab.

Here, I will just give one example of how the various symmetry elements are combined in a somewhat completed crystal.  One point that I want to emphasize in this discussion is that if 2 kinds of symmetry elements are present in the same crystal, then they will operate on each other to produce other symmetrical symmetry elements.  This should become clear as we go over the example below.

 

In this example we will start out with the crystal shown here.  Note that this crystal has rectangular-shaped sides with a square- shaped top and bottom.  The square-shaped top indicates that there must be a 4-fold rotation axis perpendicular to the square shaped face.  This is shown in the diagram.

 

 

 

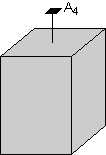Also note that the rectangular shaped face on the left side of the crystal must have a 2-fold rotation axis that intersects it.  Note that the two fold axis runs through the crystal and exits on the left-hand side (not seen in this view), so that both the left and right - hand sides of the crystal are perpendicular to a 2-fold rotation axis.

 

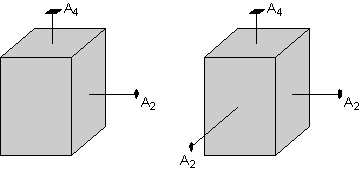Since the top face of the crystal has a 4-fold rotation axis, operation of this 4-fold rotation must reproduce the face with the perpendicular 2-fold axis on a 90o rotation.  Thus, the front and back faces of the crystal will also have perpendicular 2-fold rotation axes, since these are required by the 4-fold axis.

 

 

The square-shaped top of the crystal also suggests that there must be a 2-fold axis that cuts diagonally through the crystal.  This 2-fold axis is shown here in the left-hand diagram.  But, again operation of the 4-fold axis requires that the other diagonals also have 2-fold axis, as shown in the right-hand diagram.

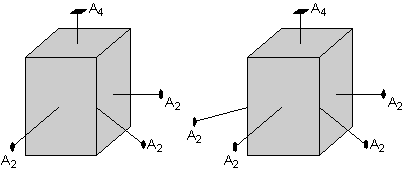Furthermore, the square-shaped top and rectangular-shaped front of the crystal suggest that a plane of symmetry is present as shown by the left-hand diagram here.  But, again, operation of the 4-fold axis requires that a mirror plane is also present that cuts through the side faces, as shown by the diagram on the right.

 

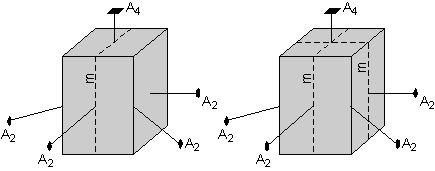The square top further suggests that there must be a mirror plane cutting the  diagonal through the crystal. This mirror plane will be reflected by the other mirror planes cutting the sides of the crystal, or will be reproduced by the 4-fold rotation axis, and thus the crystal will have another mirror plane cutting through the other diagonal, as shown by the diagram on the right. 

 

 

 

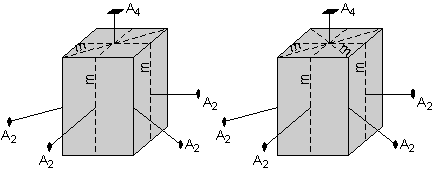Finally, there is another mirror plane that cuts through the center of the crystal parallel to the top and bottom faces.  
 

Thus, this crystal has the following symmetry elements:

  • 1  -  4-fold rotation axis (A4)
  • 4 -  2-fold rotation axes (A2), 2 cutting the faces & 2 cutting the edges.
  • 5 mirror planes (m), 2 cutting across the faces, 2 cutting through the edges, and one cutting horizontally through the center.
  • Note also that there is a center of symmetry (i).

The symmetry content of this crystal is thus: i, 1A4, 4A2, 5m
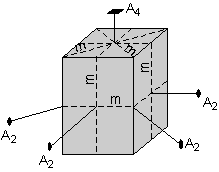If you look at Table 6.3 page120 of your text, you should see that this belongs to crystal class 4/m2/m2/m.  This class is the ditetragonal dipyramidal class. We will discuss this notation and the various crystals classes in the next lecture.

Examples of questions on this material that could be asked on an exam

  1. What is a mineral?  (Be sure you can provide an exact and thorough definition).

  2. What is the difference between an organic process and an inorganic process?

  3. Although this is just an introductory discussion of symmetry and symmetry operations and you will get more comfortable with this material as the course progresses, eventually you should be able to recognize symmetry elements in 2 dimensional drawings and 3 dimensional objects.

Return to EENS 2110 Page