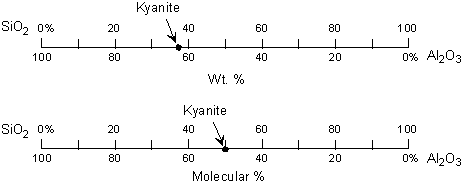
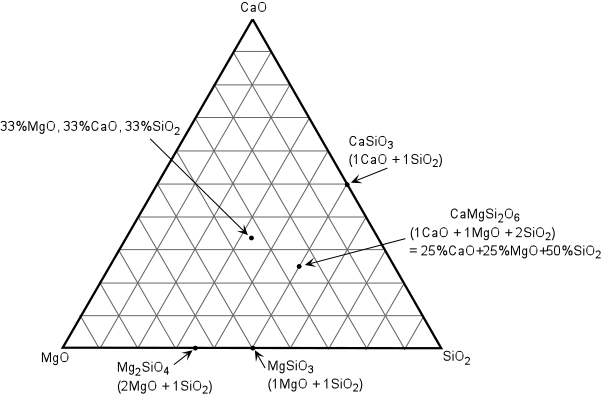
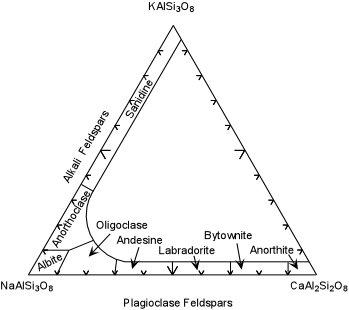
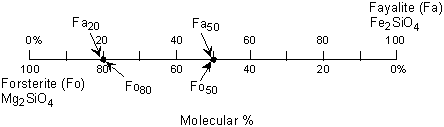| Exsolution
As mentioned above, the extent of solid solution is sometimes dependent
on temperature and pressure since the sizes of ions and the sizes of the
crystallographic sites can change with temperature and pressure.
Thus, some minerals show complete solid solution under one set of
temperature/pressure conditions, and only limited solid solution under
different temperature/pressure conditions. When the conditions change to
those where limited solid solution is favored, the mineral exsolves or
unmixes. But, because the process is taking place in the solid
state, exsolution or unmixing cannot easily form two separate phases,
because the ions must diffuse through the solid. In fact, what
happens is that two separate phases form in discrete domains within a single
mineral grain. These domains are crystallographically oriented, so
they appear as lamellae or lines across the mineral grain.
Although
we will explore this further in our discussion of phase diagrams, an
example is given here. The alkali feldspars (albite - NaAlSi3O8
- orthoclase - KAlSi3O8) form a complete solid
solution at high temperature. At lower temperature the solid
solution becomes progressively more limited, and as a result lamellae of
albite-rich feldspar begin to grow in the orthoclase-rich alkali
feldspar. This produces a texture called perthite,
where the lighter colored albite-rich feldspar is seen to occur as
irregular lines or streaks (the lamellae) within the pink orthoclase-rich
feldspar. In the case of perthite, the exsolution lamellae are often
large enough to see with the naked eye. In other systems, the
exsolution lamellae can only be observed with the petrographic microscope.
Photographic examples of exsolution lamellae can be seen in your textbook
on page 549 (fig. 12.73).
|