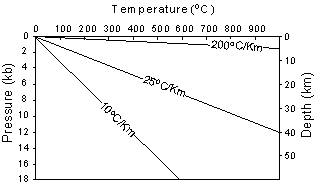
Geothermal gradients deeper in the earth become much lower than those near the surface.
| EENS 2110 |
Mineralogy |
| Tulane University |
Prof. Stephen A. Nelson |
|
Mineral Stability and Phase Diagrams |
|
|
|
As we discussed previously, there are four major processes by which
minerals form. Each of these occurs within a limited range of environmental
conditions. First, the chemical
ingredients must be present, and second, the pressure and temperature
conditions must be right. Let's first review these mineral forming
processes and the pressure temperature conditions necessary.
Thus, for any given system we can define temperature, pressure, and compositional variables that determine what minerals are stable. An understanding of mineral stability is essential in understanding which minerals form, and allow us to determine the conditions present when we encounter minerals in the Earth. |
| Recall from your physical geology course that both temperature and
pressure vary with depth in the Earth. Pressure is related to depth
because pressure is caused by the weight of the overlying rocks. The
way that pressure and temperature vary in the Earth is called the Geothermal
Gradient. |
| The average, or sometimes called normal, geothermal gradient in the
upper part of the Earth is about 25oC/km. But, the
geothermal gradient can vary from 200oC/km in areas where hot
igneous bodies are intruding at shallow levels of the crust to 10oC/km,
in areas like subduction zones where cold lithosphere descends back into
the mantle.
Geothermal gradients deeper in the earth become much lower than those near the surface. |
 |
|
Phase Diagrams A phase diagram is a graphical representation of chemical equilibrium. Since chemical equilibrium is dependent on the composition of the system, the pressure, and the temperature, a phase diagram should be able to tell us what phases are in equilibrium for any composition at any temperature and pressure of the system. First, a few terms will be defined. System - A system is that part of the universe which is under consideration. Thus, it may or may not have fixed boundaries, depending on the system. For example, if we are experimenting with a beaker containing salt and water, and all we are interested in is the salt and water contained in that beaker, then our system consists only of salt and water contained in the beaker. If the system cannot exchange mass or energy with its surroundings, then it is termed an isolated system. (Our salt and water system, if we put a lid on it to prevent evaporation, and enclosed it in a perfect thermal insulator to prevent it from heating or cooling, would be an isolated system.) If the system can exchange energy, but not mass with its surroundings, we call it a closed system. (Our beaker, still sealed, but without the thermal insulator is a closed system). If the system can exchange both mass and energy with its surroundings, we call it an open system. (Our beaker - salt - water system open to the air and not insulated is thus an open system). Phase - A phase is a physically separable part of the system with distinct physical and chemical properties. A system must consist of one or more phases. For example, in our salt-water system, if all of the salt is dissolved in the water, consists of only one phase (a sodium chloride - water solution). If we have too much salt, so that it cannot all dissolve in the water, we have 2 phases, the sodium chloride - water solution and the salt crystals. If we heat our system under sealed conditions, we might have 3 phases, a gas phase consisting mostly of water vapor, the salt crystals, and the sodium chloride - water solution. In a magma a few kilometers deep in the earth we might expect one or more phases. For example if it is very hot so that no crystals are present, and there is no free vapor phase, the magma consists of one phase, the liquid. At lower temperature it might contain a vapor phase, a liquid phase, and one or more solid phases. For example, if it contains crystals of plagioclase and olivine, these two minerals would be considered as two separate solid phases because olivine is physically and chemically distinct from plagioclase. Component - Each phase in the system may be considered to be composed of one or more components. The number of components in the system must be the minimum required to define all of the phases. For example, in our system salt and water, we might have the components Na, Cl, H, and O (four components), NaCl, H, and O (three components), NaCl and HO (two components), or NaCl-H2O (one component). However, the possible phases in the system can only consist of crystals of halite (NaCl), H2O either liquid or vapor, and NaCl-H2O solution. Thus only two components (NaCl and H2O) are required to define the system, because the third phase (NaCl - H2O solution) can be obtained by mixing the other two components. |
|
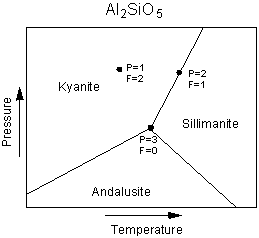
The Phase Rule The phase rule is an expression of the number of variables and equations that can be used to describe a system in equilibrium. In simple terms, the number of variables are the number of chemical components in the system plus the extensive variables, temperature and pressure. The number of phases present will depend on the variance or degrees of freedom of the system. The general form of the phase rule is stated as follows: F = C + 2 - P where F is the number of degrees of freedom or variance of the system. C is the number of components, as defined above, in the system. P is the number of phases in equilibrium, and the 2 comes from the two extensive variables, Pressure and Temperature. To see how the phase rule works, let's start with a simple one component system - the
system Al2SiO5, shown in the Pressure, Temperature phase diagram
below.
|
| First look at the point in the field of kyanite stability. Since
kyanite is the only phase present, P=1. F is 2 at this point, because one could
change both temperature and pressure by small amounts without affecting the number of
phases present. We say that this area of kyanite stability on the phase diagram is a
divariant field (variance, F =2).
Next look at the point on the phase boundary between kyanite and sillimanite. For any point on such a boundary the number of phases, P, will be 2. Using the phase rule we find that F = 1, or there is one degree of freedom. This means there is only one independent variable. |
 |
| If we change pressure, temperature must also change in
order to keep both phases stable. The phase assemblage is said to be univariant in
this case, and the phase boundaries are univariant lines (or curves in the more general
case.
Finally, we look at the point where all three univariant lines intersect. At this point, 3 phases, kyanite, andalusite, and sillimanite all coexist at equilibrium. Note that this is the only point where all three phases can coexist. For this case, P=3, and F, from the phase rule, is 0. There are no degrees of freedom, meaning that any change in pressure or temperature will result in a change in the number of phases. The three phase assemblage in a one component system is said to be invariant. |
Examples of questions on this material that could be asked on an exam
|