EENS 2110

Earth Materials
Tulane University

Prof. Stephen A. Nelson

Stereographic Projection of Crystal Faces

 

 

 

Crystallographic Angles

  
First we define the interfacial angle between two crystal faces as the angle between lines that are perpendicular to the faces.  Such a lines are called the poles to the crystal face.  Note that this angle is can be measured easily with a device called a contact goniometer.

Next, we need a systematic way to define crystallographic angles.  For this we use a spherical projection.

Imagine that we have a crystal inside of a sphere.  From each crystal face we draw a line perpendicular to the face (poles to the face).

 

 

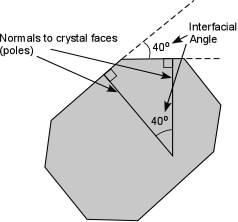
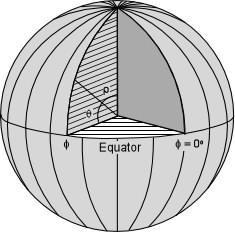
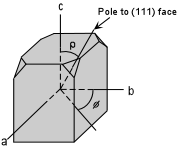
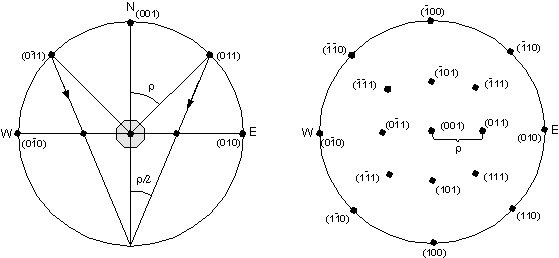
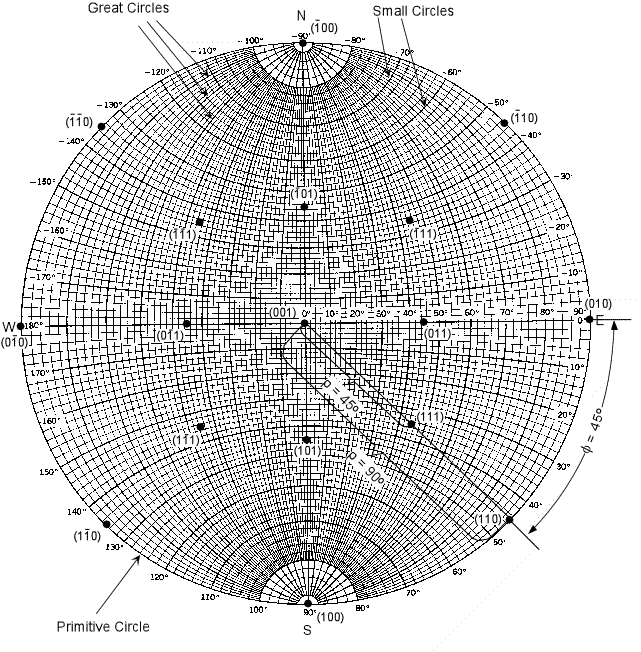
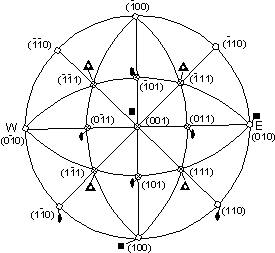
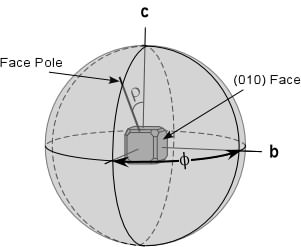
The pole to a hypothetical  (010) face will coincide with the b crystallographic axis, and will impinge on the inside of the sphere at the equator.  

We define this face (010) as having a Φ angle of 0o.  For any other face, the Φ angle will be measured from the b axis in a clockwise sense in the plane of the equator.  

We define the ρ angle, as the angle between the c axis and the pole to the crystal face, measured downward from the North pole of the sphere.  In the diagram shown here, a crystal face has a ρangle  measured in the vertical plane containing the axis of the sphere and the face pole, and a Φangle measured in the horizontal equatorial plane. Note that the (010) face has a ρangle = 90o.

 

 

Note that these angular measurements are similar to those we use for latitude and longitude to plot positions of points on the Earth's surface.  For the Earth, longitude is similar to the Φ angle, except longitude is measured from the Greenwich Meridian, defined as Φ= 0o.  Latitude is measured in the vertical plane,  up from the equator, shown as the angle q.  Thus, the ρ angle is what is called the colatitude (90o - latitude).
As an example, the ρ and Φ angles for the (111) crystal face in a crystal model is shown here.  Note again that the ρ angle is measured in the vertical plane containing the c axis and the pole to the face, and the Φ angle is measured in the horizontal plane, clockwise from the b axis.    

Generally, it is the angles of the spherical projection, ρ and Φ,  that are given for each face of a crystal.  If these are known, then the actual angles between any two faces can easily be obtained through trigonometry, or by use of the stereonet as discussed below.

Remember that it is the angular relationships between crystal faces that actually reflects the ordered internal arrangement of atoms and thus the internal symmetry upon which the external symmetry of a crystal is based.  Thus, even in distorted crystal that exhibit crystal faces, the symmetry can be determined by the angular relationships.  This is easiest to see if we invoke a method of projection of crystallographic angles called stereographic projection.

Stereographic Projection

Stereographic projection is a method used in crystallography and structural geology to depict the angular relationships between crystal faces and geologic structures, respectively.  Here we discuss the method used in crystallography, but it is similar to the method used in structural geology.

 

Imagine again that we have a crystal inside of a sphere.  This time, however we will first look at a cross-section of the sphere as shown in the left-hand diagram below.  We orient the crystal such that the pole to the (001)  face (the c axis) is vertical and points to the North pole of the sphere.  For the (011) face we draw the pole to the face to intersect the outside the of the sphere.  Then, we draw a line from the point on the sphere directly to the South Pole of the sphere.  Where this line intersects the equatorial plane is where we plot the point.  The stereographic projection then appears on the equatorial plane.

 

 

 
 

In the right hand-diagram we see the stereographic projection for faces of an isometric crystal. Note how the ρ angle is measured as the distance from the center of the projection to the position where the crystal face plots.  The Φ angle is measured around the circumference of the circle, in a clockwise direction away from the b crystallographic axis or the plotting position of the (010) crystal face. 

 

 

In order to make plotting of the stereographic projection easier, a device called a stereographic net or stereonet is used.  Such a stereonet is shown in the diagram below.  Although the North (N) and South (S) poles are shown on the stereonet, these do not correspond to the North and South Poles as defined in the projection above.  However, when plotting directional data in structural geology, they do represent the North and South geographic directions. 

 

As defined in our projection, the N and S poles would plot directly above and below the center of the stereonet.

 

 

 

 

 

 
On the stereonet, we see several different components that we define here.
  • The Primitive Circle is the circle that surrounds the stereonet. 

  • Great Circles are the curved lines that connect the points labeled N and S on the stereonet.  The E-W and N-S axes, as well as the Primitive Circle are also great circles.  Angular relationships between points can only be measured on Great Circles.

  • Small Circles are the highly curved lines that curve upward and downward on the stereonet. 

The upper faces of an isometric crystal are plotted in the stereonet above.  These faces belong to forms {100}, {110}, and {111}.  Note that the faces (111) and (110) both have a Φ angle of 45o. The ρ angle for these faces is measured along a line from the center of the stereonet (where the (001) face plots) toward the edge.  For the (111) face the ρ angle is 45o, and for the (110) face the ρ angle is 90o.

In Lab, your lab instructor will show you how to construct a stereonet for plotting crystal faces.  This will consist of a stereonet mounted on a piece of cardboard with a thumbtack through the center.  You can then place a sheet of tracing paper on the stereonet and rotate it around the thumb tack.  The following rules are then applied:
  1. All crystal faces are plotted as poles (lines perpendicular to the crystal face. Thus, angles between crystal faces are really angles between poles to crystal faces.

  2. The b crystallographic axis is taken as the starting point. Such an axis will be perpendicular to the (010) crystal face in any crystal system. The [010] axis (note zone symbol) or (010) crystal face will therefore plot at Φ = 0o and ρ = 90o.

  3. Positive Φ angles will be measured clockwise on the stereonet, and negative Φ angles will be measured counter-clockwise on the stereonet.

  4. Crystal faces that are on the top of the crystal (ρ < 90o) will be plotted as open circles, and crystal faces on the bottom of the crystal (ρ > 90o) will be plotted as "+" signs.

  5. Place a sheet of tracing paper on the stereonet and trace the outermost great circle. Make a reference mark on the right side of the circle (East).

  6. To plot a face, first measure the Φ angle along the outermost great circle, and make a mark on your tracing paper. Next rotate the tracing paper so that the mark lies at the end of the E-W axis of the stereonet.

  7. Measure the ρ angle out from the center of the stereonet along the E-W axis of the stereonet. Note that angles can only be measured along great circles. These include the primitive circle, and the E-W and N-S axis of the stereonet.
  1. Any two faces on the same great circle are in the same zone. Zones can be shown as lines running through the great circle containing faces in that zone. The zone axis can be found by setting two faces in the zone on the same great circle, and counting 90o away from the intersection of the great circle along the E-W axis.

  2. To plot symmetry axes on the stereonet, use the following conventions:

    = 2-fold axis        = 3-fold axis     = 4-fold axis     = 6-fold axis

    =  axis         = axis             = axis

 

 

 

As an example all of the faces, both upper and lower, for a crystal in the class 4/m2/m in the forms {100}(hexahedron - 6 faces), {110} (dodecahedron, 12 faces), and {111} (octahedron, 8 faces) in the stereogram to the right.  Rotation axes are indicated by the symbols as discussed above.  Mirror planes are shown as solid lines and curves, and the primitive circle represents a mirror plane.  Note how the symmetry of the crystal can easily be observed in the stereogram.

 

Return to EENS 2110 Page