EENS 2120

Petrology
Tulane University

Prof. Stephen A. Nelson

Radiometric Dating
Prior to 1905 the best and most accepted age of the Earth was that proposed by Lord Kelvin based on the amount of time necessary for the Earth to cool to its present temperature from a completely liquid state. Although we now recognize lots of problems with that calculation, the age of 25 my was accepted by most physicists, but considered too short by most geologists. Then, in 1896, radioactivity was discovered. Recognition that radioactive decay of atoms occurs in the Earth was important in two respects:
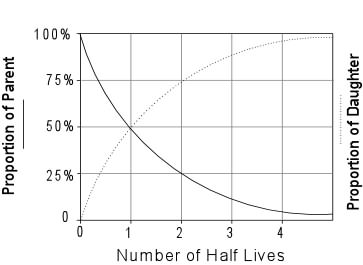
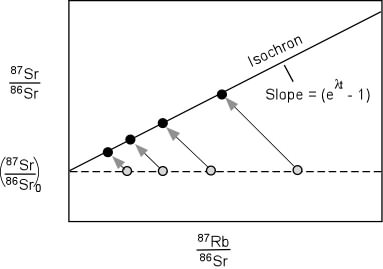
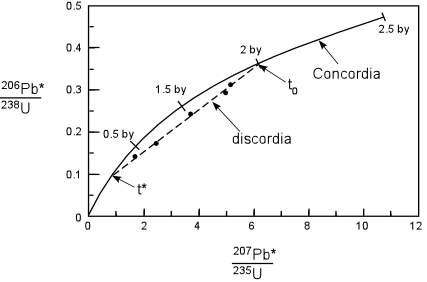
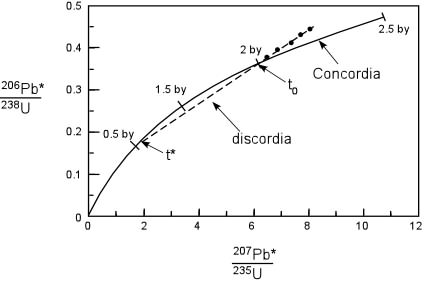
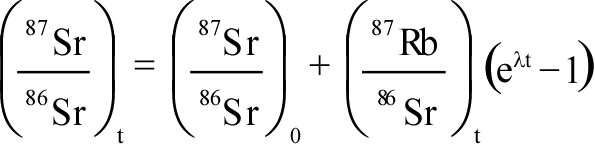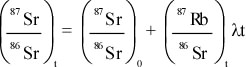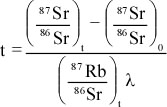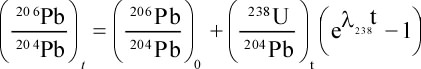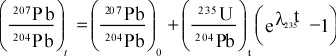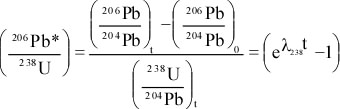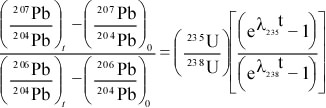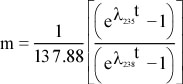  1. It provided another source of heat, not considered by Kelvin, which would mean that the cooling time would have to be much longer.

  2. It provided a means by which the age of the Earth could be determined independently.

Principles of Radiometric Dating

Radioactive decay is described in terms of the probability that a constituent particle of the nucleus of an atom will escape through the potential (Energy) barrier which bonds them to the nucleus. The energies involved are so large, and the nucleus is so small that physical conditions in the Earth (i.e. T and P) cannot affect the rate of decay.

The rate of decay or rate of change of the number N of particles is proportional to the number present at any time, i.e.

Note that dN/dt must be negative.

The proportionality constant is λ, the decay constant. So, we can write

Rearranging, and integrating, we get

or

ln(N/No) = -λ(t - to)

If we let to = 0, i.e. the time the process started, then

 

                  (1)

We next define the half-life, τ1/2, the time necessary for 1/2 of the atoms present to decay.

This is where N = N0/2.

Thus,

or 

-ln 2 = -λt,

so that
The half-life is the amount of time it takes for one half of the initial amount of the parent, radioactive isotope,  to decay to the daughter isotope.  Thus, if we start out with 1 gram of the parent isotope, after the passage of 1 half-life there will be 0.5 gram of the parent isotope left.

After the passage of two half-lives only 0.25 gram will remain, and after 3 half lives only 0.125 will remain etc.

 

Knowledge of τ1/2 or λ would then allow us to calculate the age of the material if we knew the amount of original isotope and its amount today. This can only be done for 14C, since we know N0 from the atmospheric ratio, assumed to be constant through time. For other systems we have to proceed further.

 

 

 

Some examples of isotope systems used to date geologic materials.

Parent

Daughter

τ1/2

Useful Range

 Type of Material
238U
206Pb

4.47 b.y

>10 million years 

 Igneous & sometimes metamorphic rocks and minerals
235U
207Pb

707 m.y
232Th
208Pb

14 b.y
40K
40Ar & 40Ca

1.28 b.y

>10,000 years
87Rb
87Sr

48 b.y

>10 million years
147Sm 143Nd 106 b.y.
14C
14N

5,730 y

100 - 70,000 years

 Organic Material

To see how we actually use this information to date rocks, consider the following:

Usually, we know the amount, N, of an isotope present today, and the amount of a daughter element produced by decay, D*.

By definition, 

D* = N0 - N

from equation (1)

So,

D* = Neλt-N  =  N(eλt-1)          (2)

Now we can calculate the age if we know the number of daughter atoms produced by decay, D* and the number of parent atoms now present, N. The only problem is that we only know the number of daughter atoms now present, and some of those may have been present prior to the start of our clock.

We can see how do deal with this if we take a particular case.  First we'll look at the Rb/Sr system.  

The Rb/Sr System

by β decay. The neutron emits an electron to become a proton.

For this decay reaction, λ = 1.42 x 10-11 /yr,  τ1/2 = 4.8 x 1010 yr

at present, 27.85% of natural Rb is 87Rb.

If we use this system to plug into equation (2), then

87Sr* = 87Rb (eλt-1)         (3)

but,

87Srt = 87Sr0 + 87Sr*

or

87Sr* = 87Srt - 87Sr0

Plugging this into equation (3)

87Srt = 87Sr0 + 87Rb (eλt-1)      (4)

We still don't know 87Sr0 , the amount of 87Sr daughter element initially present.

To account for this, we first note that there is an isotope of Sr, 86Sr, that is:

(1)  non-radiogenic (not produced by another radioactive decay process),

(2)  non-radioactive (does not decay to anything else).

Thus, 86Sr is a stable isotope, and the amount of 86Sr does not change through time
If we divide equation (4) through by the amount of 86Sr, then we get:
 

 

 (5)
This is known as the isochron equation.

We can measure the present ratios of (87Sr/86Sr)t and (87Rb/86Sr)t with a mass spectrometer, thus these quantities are known.

The only unknowns are thus (87Sr/86Sr)0 and t.

Note also that equation (5) has the form of a linear equation, i.e.

y = mx +b

where b, the y intercept, is (87Sr/86Sr)0 and m, the slope is (eλt - 1).

How can we use this?

 
First note that the time  t=0 is the time when Sr was isotopically homogeneous, i.e. 87Sr/86Sr was the same in every mineral in the rock (such as at the time of crystallization of an igneous rock). In nature, however, each mineral in the rock is likely to have a different amount of 87Rb. So that each mineral will also have a different 87Rb/86Sr ratio at the time of crystallization. Thus, once the rock has cooled to the point where diffusion of elements does not occur, the 87Rb in each mineral will decay to 87Sr, and each mineral will have a different 87Rb and 87Sr after passage of time.
We can simplify our isochron equation somewhat by noting that if x  is small,

so that (eλt - 1) = λt, when λt is small. 
So, applying this simplification,

 

 (6)

and solving for t

The initial ratio, (87Sr/86Sr)0, is useful as a geochemical tracer. The reason for this is that Rb has become distributed unequally through the Earth over time.

For example the amount of Rb in mantle rocks is generally low, i.e. less than 0.1 ppm. The mantle thus has a low 87Rb/86Sr ratio and would not change its 87Sr/86Sr ratio very much with time.

Crustal rocks, on the other hand generally have higher amounts of Rb, usually greater than 20 ppm, and thus start out with a relatively high 87Rb/86Sr ratio. Over time, this results in crustal rocks having a much higher 87Sr/86Sr ratio than mantle rocks.

Thus if the mantle has a 87Sr/86Sr of say 0.7025, melting of the mantle would produce a magma with a 87Sr/86Sr ratio of 0.7025, and all rocks derived from that mantle would have an initial 87Sr/86Sr ratio of 0.7025.

On the other hand, if the crust with a 87Sr/86Sr of 0.710 melts, then the resulting magma would have a 87Sr/86Sr of 0.710 and rocks derived from that magma would have an initial 87Sr/86Sr ratio of 0.710.

Thus we could tell whether the rock was derived from the mantle or crust be determining its initial Sr isotopic ratio as we discussed previously in the section on igneous rocks.

 

The U, Th, Pb System

Two isotopes of Uranium and one isotope of Th are radioactive and decay to produce various isotopes of Pb. The decay schemes are as follows

 

1. by α decay

λ238 = 1.551 x 10-10/yr, τ1/2 = 4.47 x 109 yr

2. 

λ235 = 9.849 x 10-10/yr, τ1/2 = 0.707 x 109 yr

Note that the present ratio of 

3.

λ232 = 4.948 x 10-11/yr, τ1/2 = 1.4 x 1010 yr

232Th has such along half life that it is generally not used in dating.

204Pb is a stable non-radiogenic isotope of Pb, so we can write two isochron equations and get two independent dates from the U - Pb system.

 

 (7) and

 

 (8)

If these two independent dates are the same, we say they are concordant.

We can also construct a Concordia diagram, which shows the values of Pb isotopes that would give concordant dates. The Concordia curve can be calculated by defining the following:

         (9)

and

    (10)

We can plug in t and solve for the ratios 206Pb*/238U and 207Pb*/235U to define a curve called the Concordia. 

The Concordia is particularly useful in dating of the mineral Zircon (ZrSiO4).  Zircon has a high hardness (7.5) which makes it resistant to mechanical weathering, and it is also very resistant to chemical weathering.  Zircon can also survive metamorphism.  Chemically, zircon usually contains high amounts of U and low amounts of Pb, so that large amounts of radiogenic Pb are produced.  Other minerals that also show these properties, but are less commonly used in radiometric dating are Apatite and sphene.  

If a zircon crystal originally crystallizes from a magma and remains a closed system (no loss or gain of U or Pb)  from the time of crystallization to the present, then the 206Pb*/238U and 207Pb*/235U ratios in the zircon will plot on the Concordia and the age of the zircon can be determined from its position on the plot.

Discordant dates will not fall on the Concordia curve.

Sometimes, however, numerous discordant dates from the same rock will plot along a line representing a chord on the Concordia diagram. Such a chord is called a discordia.

 

 
The discordia is often interpreted by extrapolating both ends to intersect the Concordia. The older date, t0 is then interpreted to be the date that the system became closed, and the younger date, t*, the age of an event (such as metamorphism) that was responsible for Pb leakage. Pb leakage is the most likely cause of discordant dates, since Pb will be occupying a site in the crystal that has suffered radiation damage as a result of U decay.  U would have been stable in the crystallographic site, but the site is now occupied by by Pb.  An event like metamorphism could heat the crystal to the point where Pb will become mobile.  
Another possible scenario involves U leakage, again possibly as a result of a metamorphic event.  U leakage would cause discordant points to plot above the cocordia.  But, again, exptrapolation of the discordia back to the two points where it intersects the Concordia, would give two ages - t* representing the possible metamorphic event and t0 representing the initial crystallization age of the zircon.

We can also define what are called Pb-Pb Isochrons by combining the two isochron equations (7) and (8).

      (11)

Since we know that the , and assuming that the 206Pb and 207Pb dates are the same, then equation (11) is the equation for a family of lines that have a slope

that passes through the point 

 

The Age of the Earth

  1. A minimum age of the Earth can be obtained from the oldest known rocks on the Earth. So far, the oldest rock found is a tonalitic Gneiss (metamorphic rock) rock from the Northwest Territories, Canada, with an age of 3.962 Billion ± 3 million years.  This gives us only a minimum age of the Earth. Is it likely that we will find a rock formed on the Earth that will give us the true age of the Earth?

  2. An estimate can be obtained from arguments in nuclear physics, which says that the  235U/238U ratio may have been 1.0 when the elements formed. Thus, since

 

 

we can write

 

 

or

 

 

 

and solve for t . The answer is about 6 billion years.

This argument tells when the elements were formed that make up the Earth, but does not really give us the age of the Earth. It does, however, give a maximum age of the Earth.

  1. From the Pb-Pb isochron equation (11) we can make some arguments about meteorites. First, it appears that meteorites have come from somewhere in the solar system, and thus may have been formed at the same time the solar system (and thus the Earth) formed.

    If all of the meteorites formed at the same time and have been closed to U and Pb since their formation, then we can use the Pb-Pb isochron to date all meteorites. First, however, we need to know the initial ratios of the Pb isotopes.

    We recognize two major types of meteorites:

    Fe- meteorites and stony (or chondritic) meteorites

    The Fe meteorites contain the mineral troilite (FeS) that has no U. Since the mineral troilite contains no U, all of the Pb present in the troilite is the Pb originally present, and none of it has been produced by U decay. Thus, the troilite in the Fe-meteorites will give us the initial ratios of 206Pb/204Pb and 207Pb/204Pb.

    We can then determine the Pb ratios in other meteorites and see if they fall on a Pb-Pb isochron that passes through the initial ratios determined from troilite in Fe-meteorites.

    The slope of this isochron, known as the Geochron, gives an age of 4.55 ± 0.07 x 109 yrs.
 

 

Is this the age of the Earth?

Lunar rocks also lie on the Geochron, at least suggesting that the moon formed at the same time as meteorites.

Modern Oceanic Pb - i.e. Pb separated from continents and thus from average crust also plots on the Geochron, and thus suggests that the Earth formed at the same time as the meteorites and moon.

Thus, our best estimate of the age of the Earth is 4.55 billion years.

Other Dating Methods

Sm - Nd Dating

147Sm → 143Nd

λ = 6.54 x 10-12 /yr, τ1/2 = 1.06 x 1011 yr

144Nd is stable and non-radiogenic, so we can write the isochron equation as:

 

The isochron equation is applied just like that for the Rb-Sr system, by determining the 143Nd/144Nd and 147Sm/144Nd ratios on several minerals with a mass spectrometer and then from the slope determine the age of the rock.

The initial ratio has particular importance for studying the chemical evolution of the Earth's mantle and crust, as we discussed in the section on igneous rocks.

 

 

K-Ar Dating

40K is the radioactive isotope of K, and makes up 0.119% of natural K. Since K is one of the 10 most abundant elements in the Earth's crust, the decay of 40K is important in dating rocks. 40K decays in two ways:

 

  40K → 40Ca by β decay. 89% of follows this branch.

But this scheme is not used because 40Ca can be present as both radiogenic and non-radiogenic Ca.

   40K →  40Ar by electron capture

For the combined process,

λ = 5.305 x 10-10/ yr ,τ1/2 = 1.31 x 109 yr

and for the Ar branch of the decay scheme

λe = 0.585 x 10-10/ yr

Since Ar is a noble gas, it can escape from a magma or liquid easily, and it is thus assumed that no 40Ar is present initially. Note that this is not always true. If a magma cools quickly on the surface of the Earth, some of the Ar may be trapped. If this happens, then the date obtained will be older than the date at which the magma erupted. For example lavas dated by K-Ar that are historic in age, usually show 1 to 2 my old ages due to trapped Ar. Such trapped Ar is not problematical when the age of the rock is in hundreds of millions of years.

The dating equation used for K-Ar is:

where = 0.11 and refers to fraction of 40K that decays to 40Ar.
Some of the problems associated with K-Ar dating are
  1. Excess argon. This is only a problem when dating very young rocks or in dating whole rocks instead of mineral separates. Minerals should not contain any excess Ar because Ar should not enter the crystal structure of a mineral when it crystallizes. Thus, it always better to date minerals that have high K contents, such as sanidine or biotite. If these are not present, Plagioclase or hornblende. If none of these are present, then the only alternative is to date whole rocks.
      
  2.  Atmospheric Argon. 40Ar is present in the atmosphere and has built up due to volcanic eruptions. Some 40Ar could be absorbed onto the sample surface. This can be corrected for.
      
  3.  Metamorphism or alteration. Most minerals will lose Ar on heating above 300oC - thus metamorphism can cause a loss of Ar or a partial loss of Ar which will reset the atomic clock. If only partial loss of Ar occurs then the age determined will be in between the age of crystallization and the age of metamorphism. If complete loss of Ar occurs during metamorphism, then the date is that of the metamorphic event. The problem is that there is no way of knowing whether or not partial or complete loss of Ar has occurred.
14Carbon Dating

Radiocarbon dating is different than the other methods of dating because it cannot be used to directly date rocks, but can only be used to date organic material produced by once living organisms.

 

  •   14C is continually being produced in the Earth's upper atmosphere by bombardment of 14N by cosmic rays. Thus the ratio of 14C to 14N in the Earth's atmosphere is constant.
     
     
  • Living organisms continually exchange Carbon and Nitrogen with the atmosphere by breathing, feeding, and photosynthesis. Thus, so long as the organism is alive, it will have the same ratio of  14C to 14N as the atmosphere.
      
  • When an organism dies, the 14C decays back to 14N, with a half-life of 5,730 years.  Measuring the amount of 14C in this dead material thus enables the determination of the time elapsed since the organism died.
      
  • Radiocarbon dates are obtained from such things as bones, teeth, charcoal, fossilized wood, and shells.
     
     Because of the short half-life of 14C, it is only used to date materials younger than about 70,000 years.
Other Uses of Isotopes
  1. Radioactivity is an important heat source in the Earth. Elements like K, U, Th, and Rb occur in quantities large enough to release a substantial amount of heat through radioactive decay. Thus radioactive isotopes have potential as fuel for such processes as mountain building, convection in the mantle to drive plate tectonics, and convection in the core to produce the Earth's magnetic Field.
      
  2.  Initial isotopic ratios are useful as geochemical tracers. Such tracers can be used to determine the origin of magmas and the chemical evolution of the Earth.
      
  3.  Short-lived isotopes (Isotopes made during nucleosynthesis that have nearly completely decayed away) can give information on the time elapsed between nucleosynthesis and Earth Formation. 
      
  4.  Ratios of stable, low mass isotopes, like those of O, S, C, and H can be used as tracers, as well as geothermometers, since fractionation of light isotopes can take place as a result of chemical process. We can thus use these ratios of light isotopes to shed light on processes and temperatures of past events.
      
  5.  Radioactivity is a source of energy and thus can be exploited for human use - good and bad.

Examples of questions on this material that could be asked on an exam

  1. Which isotopic systems are most useful for radiometric dating and what are the limitations of each?

  2. What is an isochron and what information can be obtained from an isochron?

  3. Why is zircon the preferred mineral for obtainting U - Pb dates?

  4. What is the Concordia, how is it used, and what information can be obtained from discordant dates?

  5. How is K-Ar dating different from U-Pb, Rb-Sr, and Nd-Sm dating?

  6. How does radiocarbon dating differ from the other methods of radiometric dating?

Return to EENS 2120 Home Page