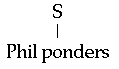
In this chapter, we jump straight into the mechanics of semantic analysis by adopting a formalism known as T (for truth) theory. What T theory does is deduce the truth of a sentence S from some condition p, by means of rules of the form: S is true if and only if p.
A T theory consists of two components. The first tells us what strings of words are interpretable. The second tells us how interpretable strings are interpreted, that is, whether they are true or not. The first one is called the syntactic component, and the second one, the semantic component.
The syntactic component of our first bit of English contains three basic sentences, two rules for connecting sentences, and one rule for creating negative sentences. The rules are stated with the help of an arrow, for instance 'S -> Phil ponders'. The arrow is usually pronounced "rewrites as", so the example would be read as "S rewrites as 'Phil ponders'". There is also a convention for diagraming such rules by putting the left-hand side of the arrow at the top, a line from it going straight down, and the right-hand side of the arrow underneath:
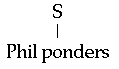
An alternative to drawing out these diagrams is to treat the left-hand side of the arrow as a label, and to attach it as a subscript to the inside edges of square brackets:
Since English is read left to right, the trailing label - the second one - is usually omitted as redundant.
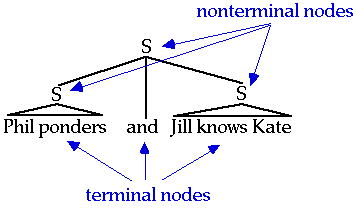
Since the rules provide a means for creating complex sentences out of basic ones, these conventions for diagraming and bracketing strings can produce rather complicated objects. Here's an example that is slightly different from the book's, with the parts labeled with some new terminology:
The interpretation of these sentences is defined by a separate set of rules, of the form mentioned above: S is true if and only if p.
Finally, there is a set of rules that shows us how to draw inferences from interpreted sentences, known as production rules.
The odd thing about a T theory is that it does not explain what a sentence means; it only explains under what conditions a sentence is true. To make the step from truth to meaning requires that the two expressions paired by "is true if and only if" (the right- and left-hand sides of the arrows) can be equated with the two expressions paired by "means that". A T theory that supports that equivalence is called an interpretive T theory.
The challenge is to find a T theory that provides an interpretive T theorem for every sentence of the object language without providing uninterpretive T theorems for any sentence. That is, the T theory must produce just enough T theorems - not too few, and not too many:
The latter is an uninterpretive T theorem because "Jill knows Kate" does not mean anything that has to do with whether 2 plus 2 equals 4.
Both of these requirements may seem so obvious as to not deserve mentioning, but in fact the deductive systems of standard logic are wildly overproductive.
As defined so far, an interpretive T theory in its formulation does not give any information about the meaning of sentences. But meaningfulness can be imposed by assuming that the biological endowment of humans obliges them to learn interpretive T theories (pp. 39-40):
The latter is extremely tricky and seems to be a combination of universal grammar + context of language acquisition.
Disquotational vs nondisquotational theories
A noncompositional T theory
Previous class |
Next class |