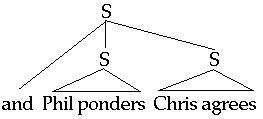
- [and S1 S2] is true iff S1 is true and S2 is true.
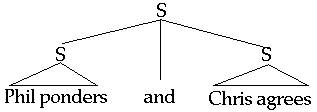
- [S1 and S2] is true iff S1 is true and S2 is true.
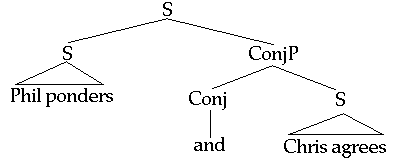
- [S1 [and S2]] is true iff S1 is true and S2 is true.
Summary
The first issue of the chapter is to sketch three possible structures for sentences made out of conjunctions and negations.Taking the case of sentences made out of the conjunction and, the three structures are:



The challenge, then, is to find a way to choose among these alternatives.
One way is by assuming that structures converge across linguistic components. [What are the linguistic components?] There are three reasons for suspecting that structures might converge:
In contrast, linguistic structure, especially semantics, may not converge with logical structure. The main reason for suspecting such a divergence is that logicosemantic relations between sentences are not defined in the object language, but rather in the metalanguage.
Strong compositionality hypothesis: R is a possible semantic rule for a human language only if R is strictly local [in scope] and purely interpretive [in contribution].
Now consider the two grammars that we have been assuming:
S -> S or S S -> it is not the case that S |
S -> S ConjP |
A semantic rule is exhaustive if it assigns a semantic value to every constituent of a node.
Previous class |
Next class |