Sound¶
Introduction¶
I made a sound file which contains wind, a meadowlark singing, a bell dinging and me saying “To be or not to be, that is the question”. I open it in Praat to the following screen; you can download it yourself from if you want to follow along at home.
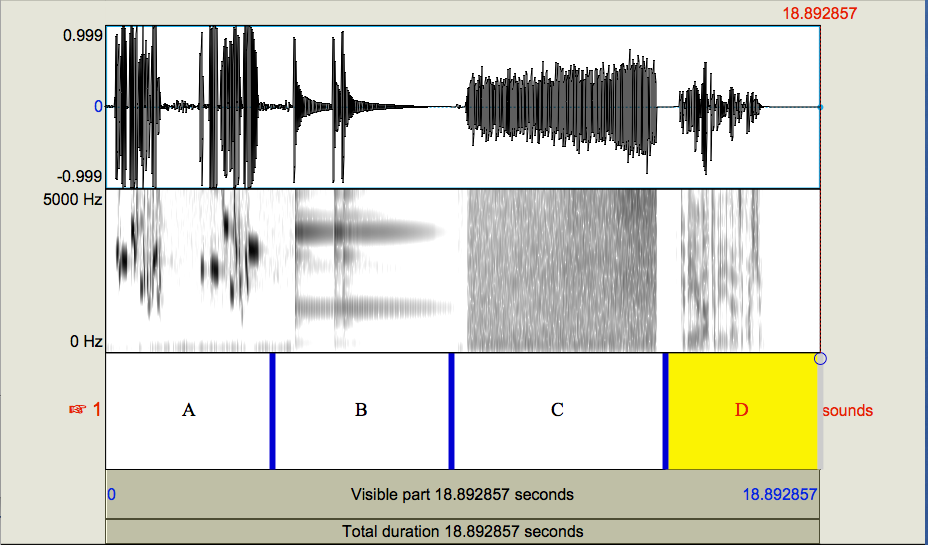
Fig. 11 Four sounds¶
From http://soundbible.com/, 2190-Front-Desk-Bell and 2180-Meadowlark by Daniel Simon, 1234-Wind by Mike Koenig.
Questions
Which graph A through D corresponds to which sound?
The physics of sound¶
Sound is generally considered to have three physical attributes: frequency, strength or intensity, and quantity.
Intensity¶
Intensity is the attribute of a sound that allows it to be ordered on a scale from quiet to loud. Sound intensity is also known as sound pressure, sound power or sound strength. It is usually measured as the sound pressure level or SPL in decibels. Let’s unpack that.
A decibel is one tenth of a bel. A bel is the ratio of the absolute measure of power or intensity to a reference value. For sound pressure level, the reference value is the threshold of human hearing. The ratio is measured logarithmically, so that an increase of 10 db means that intensity has increased 100 times. The ‘thermometer’ below plots some common sounds on a deciBel scale in terms of their loudness. There are many others that you can find by googling “db scale hearing”:

Fig. 12 The intensity of some common sounds in dB.¶
Quantity¶
The quantity of a sound is how long it lasts. It is measured in seconds. And that is all there is to say about it.
The psychology of sound¶
Even though sound is measured physically in three ways, it is perceived in at least six: pitch, loudness, phase, direction, distance, and timbre. We touch on each.
Pitch is the perception of a sound as being high or low and comes from its frequency, so the two are used interchangeably.
References¶
Powerpoint and podcast¶
The next topic¶
Come to class having read Speech sounds and their articulation and answered the questions.
Last edited: Sep 19, 2021